
【题目】如图,![]() ,
,![]() ,
,![]() 的平分线与
的平分线与![]() 的平分线交于点
的平分线交于点![]() ,则
,则![]() 的度数是________.
的度数是________.
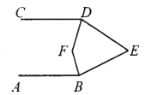
【答案】![]()
【解析】
过点E作EG∥AB,过点F作FP∥AB,根据平行线的性质可得∠ABE+∠BEG=180°,∠GED+∠EDC=180°,根据角的计算以及角平分线的定义可得∠FBE+∠EDF=![]() (∠ABE+∠CDE),再依据∠ABF=∠BFP,∠CDF=∠DFP结合角的计算即可得出结论.
(∠ABE+∠CDE),再依据∠ABF=∠BFP,∠CDF=∠DFP结合角的计算即可得出结论.
解:如图,过点E作EG∥AB,过点F作FP∥AB,
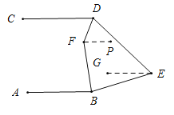
∵AB∥CD,
∴AB∥CD∥GE∥FP
∴∠ABE+∠BEG=180°,∠GED+∠EDC=180°,
∴∠ABE+∠CDE+∠BED=360°;
又∵∠BED=60°,
∴∠ABE+∠CDE=300°.
∵∠ABE和∠CDE的平分线相交于F,
∴∠ABF+∠CDF=![]() (∠ABE+∠CDE)=150°,
(∠ABE+∠CDE)=150°,
∵FP∥AB,AB∥CD,
∴AB∥CD∥FP,
∴∠ABF=∠BFP,∠CDF=∠DFP
∴∠BFD=∠BFP+∠DFP=∠ABF+∠CDF =150°.
故答案为:150°.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】 (用如图所示的曲尺形框框(有三个方向),可以套住下表中的三个数,设被框住的三个数中(第一个框框住的最小的数为a、第二个框框住的最小的数为b、第三个框框住的最小的数为c).
(1)第一个框框住的三个数中最小的数为a,三个数的和是: ;第二个框框住的三个数中最小的数为b,三个数的和是: ;第三个框框住的三个数中最小的数为c,三个数的和是: ;
(2)这三个框框住的数的和能是48吗?,能,求出最小的数a、b、c的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是( )
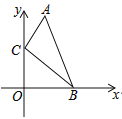
A. (0,0); B. (0,1); C. (0,2); D. (0,3).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高新一中初中校区名校+教育联合体主题美术展在西安高新区都市之门举办,学校组织七年级部分学生乘车参观展览,若用2辆小客车和1辆大客车,则每次可运送学生95人;若用1辆小客车和2辆大客车,则每次可运送学生115人(注意:每辆小客车和大客车都坐满).
(1)每辆小客车和大客车各能坐多少人?
(2)若现在要运送500名学生,计划租用小客车![]() 辆,大客车
辆,大客车![]() 辆,一次送完,且恰好每辆车都坐满,请你帮学校设计出所有的租车方案.
辆,一次送完,且恰好每辆车都坐满,请你帮学校设计出所有的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应党的“文化自信”号召,某校开展了古诗词诵读大赛活动,现随机抽取部分同学的成绩进行统计,并绘制成如下的两个不完整的统计图,请结合图中提供的信息,解答下列问题:
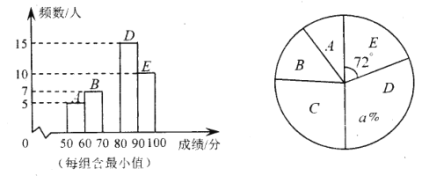
(1)填空:样本容量为________,![]() ________;
________;
(2)把频数分布直方图补充完整;
(3)求扇形![]() 的圆心角度数;
的圆心角度数;
(4)如果全校有2000名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀奖的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“五一”期间,某公司组织318名员工到雷山西江千户苗寨旅游,旅行社承诺每辆车安排有一名随团导游,并为此次旅行安排8名导游,现打算同时租甲、乙两种客车,其中甲种客车每辆载客45人,乙种客车每辆载客30人.
(1)请帮助旅行社设计租车方案.
(2)若甲种客车租金为800元/辆,乙种客车租金为600元/辆,旅行社按哪种方案租车最省钱?此时租金是多少?
(3)旅行前,旅行社的一名导游由于有特殊情况,旅行社只能安排7名导游随团导游,为保证所租的每辆车安排有一名导游,租车方案调整为:同时租65座、45座和30座的大小三种客车,出发时,所租的三种客车的座位恰好坐满,请问旅行社的租车方案如何安排?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是一个非常重要的数学工具,通过它把数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.已知数轴上有点A和点B,点A和点B分别表示数-20和40,请解决以下问题:
(1)请画出数轴,并标明A、B两点;
(2)若点P、Q分别从点A、点B同时出发,相向而行,点P、Q移动的速度分别为每秒4个单位长度和2个单位长度.问:当P、Q相遇于点C时,C所对应的数是多少?
(3)若点P、Q分别从点A、点B同时出发,沿x轴正方向同向而行,点P、Q移动的速度分别为每秒4个单位长度和2个单位长度.问:当P、Q相遇于点D时,D所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,原点为O,已知一次函数的图象过点A(0,5),点B(﹣1,4)和点P(m,n)
(1)求这个一次函数的解析式;
(2)当n=2时,求直线AB,直线OP与x轴围成的图形的面积;
(3)当△OAP的面积等于△OAB的面积的2倍时,求n的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com