
����Ŀ��Ϊ��Ӧ���ġ��Ļ����š����٣�ijУ��չ�˹�ʫ���ж���������������ȡ����ͬѧ�ijɼ�����ͳ�ƣ������Ƴ����µ�������������ͳ��ͼ������ͼ���ṩ����Ϣ������������⣺
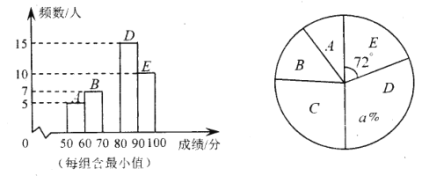
(1)��գ���������Ϊ________��![]() ________��
________��
(2)��Ƶ���ֲ�ֱ��ͼ����������
(3)������![]() ��Բ�ĽǶ�����
��Բ�ĽǶ�����
(4)���ȫУ��2000��ѧ���μ���λ��90������(��90��)Ϊ���㣬��ô���ƻ�����㽱��ѧ���ж����ˣ�
���𰸡�(1)50��30��(2)��������(3)![]() ��(4)400��.
��(4)400��.
��������
��1���ȸ���E�ȼ���������ռ�������ı����ɵ�������������D�ȼ����������������ɵ�a��ֵ������������ȥ�������ȼ��������C�ȼ������ɲ�ȫͼ�Σ�
��2����360������A�ȼ�������ռ�����ɵã�
��3��������������������E�ȼ�������ռ������
�⣺��1���߱������������Ϊ10��![]() =50���ˣ���
=50���ˣ���
��D�ȼ�������ռ�ٷֱ�a%=![]() ��100%=30%����a=30��
��100%=30%����a=30��
C�ȼ�����Ϊ50-��5+7+15+10��=13�ˣ�
��ȫͼ�����£�
�ʴ�Ϊ��30��
��2������B��Բ�ĽǶ���Ϊ360���![]() =50.4����
=50.4����
��3�����ƻ�����㽱��ѧ����2000��![]() =400�ˣ�
=400�ˣ�


 �ο�������ϵ�д�
�ο�������ϵ�д� ������ѧ��ʱ��ҵϵ�д�
������ѧ��ʱ��ҵϵ�д� ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=a��x+3����x��1����a��0������x��������������ཻ��A��B���㣬��y���ཻ�ڵ�C��������A��ֱ��y=��![]() x+b�������ߵ���һ������ΪD��
x+b�������ߵ���һ������ΪD��
��1������D�ĺ�����Ϊ2���������ߵĺ�������ʽ��
��2�����ڵ��������ڵ����������е�P��ʹ����A��B��PΪ��������������ABC���ƣ����P�����ꣻ
��3���ڣ�1���������£����E���߶�AD�ϵ�һ�㣨�����˵㣩������BE��һ����Q�ӵ�B���������߶�BE��ÿ��1����λ���ٶ��˶�����E�������߶�ED��ÿ��![]() ����λ���ٶ��˶�����D��ֹͣ���ʵ���E�������Ƕ���ʱ����Q�������˶�����������ʱ�����٣�
����λ���ٶ��˶�����D��ֹͣ���ʵ���E�������Ƕ���ʱ����Q�������˶�����������ʱ�����٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ������⣺
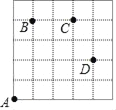
��ͼ��һֻ�׳���5��5�ķ���ÿ������߳���Ϊ1�����������������У������ǹ涨������ͼ�����У����ϣ������ң� ���м�Ϊ��+�������£������� ���м�Ϊ�����������ҵ�һ������ʾ���ҷ��ڶ�������ʾ���·���
���磺��A��B��Ϊ��A��B��+1��+4������D��C��Ϊ��D��C����1��+2����
˼����Ӧ�ã�
��1��ͼ��A��C���� ������ ������B��C���� ������ ������D��A���� ������ ����
��2�����׳��A��P������·������Ϊ����+3��+2������+1��+3������+1����2��������ͼ�б��P��λ�ã�
��3�����׳������·��ΪA����+1��+4������+2��0������+1����2��������4����2���������ü׳��߹�����·�̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����AOB=120�㣬CE��BD��DE��AC����AD=4�����ı���CODE���ܳ� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
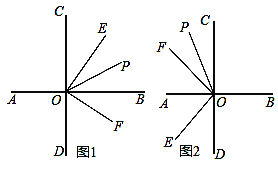
����Ŀ����ֱ֪��CD��AB�ڵ�O����EOF��90�㣬����OPƽ�֡�COF��
��1����ͼ1����EOF��ֱ��CD���Ҳࣺ
������COE��30�㣬���BOF�͡�POE�Ķ�����
�����жϡ�POE���BOP֮�����������������ϵ����˵�����ɣ�
��2����ͼ2����EOF��ֱ��CD����࣬�ҵ�E�ڵ�F���·���
����ֱ��д����POE���BOP֮���������ϵ��
����ֱ��д����POE���DOP֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�У�ABΪֱ����OC��AB����CD��OB���ڵ�F������D��A�ֱ�����O�����߽��ڵ�G������AB�ӳ��߽��ڵ�E��
��1����֤����1=��2��
��2����֪��OF��OB=1��3����O�İ뾶Ϊ3����AG�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��ƽ��ֱ������ϵ��,����B(6,0)��ֱ��AB��ֱ��OA�ཻ�ڵ�A(4,2)����y���ཻ�ڵ�C������M���߶�OA������AC���˶���
(1)��ֱ��AB�Ľ���ʽ��
(2)����OMC���������OAC�������![]() ����ֱ��д����ʱ��M������ .
����ֱ��д����ʱ��M������ .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ǽס�������ͬһ�ص������·����ʱ��仯��ͼ��

��1�����������У� ���Ա����� ���������
��2�����ٶ� �ҵ��ٶȣ���<��=����>����
��3��·��Ϊ150kmʱ������ʻ�� Сʱ������ʻ�� Сʱ��
��4���ױ��������� Сʱ����9ʱ�� ����ǰ�档
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com