
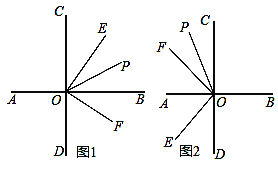
【题目】已知直线CD⊥AB于点O,∠EOF=90°,射线OP平分∠COF.
(1)如图1,∠EOF在直线CD的右侧:
①若∠COE=30°,求∠BOF和∠POE的度数;
②请判断∠POE与∠BOP之间存在怎样的数量关系?并说明理由.
(2)如图2,∠EOF在直线CD的左侧,且点E在点F的下方:
①请直接写出∠POE与∠BOP之间的数量关系;
②请直接写出∠POE与∠DOP之间的数量关系.
【答案】(1)①∠BOF= 30°,∠POE=30°,②∠POE=∠BOP(2)①∠POE=∠BOP②∠POE+∠DOP=270°
【解析】
(1)①根据余角的性质得到∠BOF=∠COE=30°,求得∠COF=90°+30°=120°,根据角平分线的定义即可得到结论;
②根据垂线的性质和角平分线的定义即可得到结论;
(2)①根据角平分线的定义得到∠COP=∠POF,求得∠POE=90°+∠POF,∠BOP=90°+∠COP,于是得到∠POE=∠BOP;
②根据周角的定义即可得到结论.
(1)①∵CD⊥AB,
∴∠COB=90°,
∵∠EOF=90°,
∴∠COE+∠BOE=∠BOE+∠BOF=90°,
∴∠BOF=∠COE=30°,
∴∠COF=90°+30°=120°,
∵OP平分∠COF,
∴∠COP=![]() ∠COF=60°,
∠COF=60°,
∴∠POE=∠COP﹣∠COE=30°;
②CD⊥AB,
∴∠COB=90°,
∵∠EOF=90°,
∴∠COE+∠BOE=∠BOE+∠BOF=90°,
∴∠BOF=∠COE,
∵OP平分∠COF,
∴∠COP=∠POF,
∴∠POE=∠COP﹣∠COE,∠BOP=∠POF﹣∠BOF,
∴∠POE=∠BOP;
(2)①∵∠EOF=∠BOC=90°,
∵PO平分∠COF,
∴∠COP=∠POF,
∴∠POE=90°+∠POF,∠BOP=90°+∠COP,
∴∠POE=∠BOP;
②∵∠POE=∠BOP,∠DOP+∠BOP=270°,
∴∠POE+∠DOP=270°.


科目:初中数学 来源: 题型:
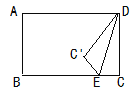
【题目】如图,矩形ABCD中,CD=6,E为BC边上一点,且EC=2将△DEC沿DE折叠,点C落在点C'.若折叠后点A,C',E恰好在同一直线上,则AD的长为( )
A.8B.9C.![]() D.10
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知抛物线![]() 与直线
与直线![]() 的一个交点记为A,点A的横坐标是-3.
的一个交点记为A,点A的横坐标是-3.

(1)求抛物线M1的表达式及它的顶点坐标;
(2)将抛物线![]() 向右平移3个单位,再向上平移3个单位,得到抛物线M2,直线
向右平移3个单位,再向上平移3个单位,得到抛物线M2,直线![]() 与M2的一个交点记为B,点C是线段AB上的一个动点,过点C作x轴的垂线,垂足为D,在CD的右侧作正方形CDEF.
与M2的一个交点记为B,点C是线段AB上的一个动点,过点C作x轴的垂线,垂足为D,在CD的右侧作正方形CDEF.
①当点C的横坐标为2时,直线y=x+n恰好经过正方形CDEF的顶点F,求此时n的值;
②在点C的运动过程中,若直线y=x+n与正方形CDEF始终没有公共点,求n的取值范围(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应党的“文化自信”号召,某校开展了古诗词诵读大赛活动,现随机抽取部分同学的成绩进行统计,并绘制成如下的两个不完整的统计图,请结合图中提供的信息,解答下列问题:
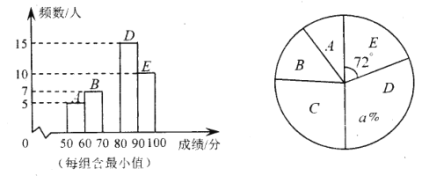
(1)填空:样本容量为________,![]() ________;
________;
(2)把频数分布直方图补充完整;
(3)求扇形![]() 的圆心角度数;
的圆心角度数;
(4)如果全校有2000名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀奖的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)+3+(-5)
(2)-89-11
(3)(﹣5.5)+(﹣3.2)﹣(﹣2.5)﹣4.8
(4)17﹣(﹣8)×(﹣2)+4×(﹣3)
(5)(-32![]() )-[5
)-[5![]() -(+3
-(+3![]() )+(-5
)+(-5![]() )+(-2
)+(-2![]() )]
)]
(6)(![]() )×(﹣12)
)×(﹣12)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=kx+b交x轴于点A,交y轴于点B,直线y=2x﹣4交x轴于点D,与直线AB相交于点C(3,2).
(1)根据图象,写出关于x的不等式2x﹣4>x+b的解集;
(2)若点A的坐标为(5,0),求直线AB的解析式;
(3)在(2)的条件下,求四边形BODC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,四边形ABCD是正方形,点G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F.
(1)求证:DEBF=EF;
(2)若点G为CB延长线上一点,其余条件不变。请你在图②中画出图形,写出此时DE、BF、EF之间的数量关系(不需要证明);

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角项点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
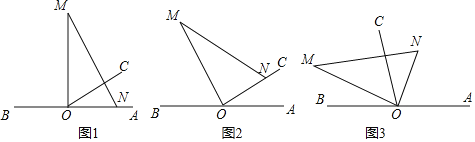
(1)将图1中的三角板绕点O以每秒5°的速度沿逆时针方向旋转一周.如图2,经过t秒后,ON落在OC边上,则t= 秒(直接写结果).
(2)在(1)的条件下,若三角板继续转动,同时射线OC也绕O点以每秒10°的速度沿逆时针方向旋转一周,当OC转动9秒时,求∠MOC的度数.
(3)在(2)的条件下,它们继续运动多少秒时,∠MOC=35°?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com