
����Ŀ����ͼ1��OΪֱ��AB��һ�㣬����O������OC����AOC��30������һֱ�����ǰ壨��M��30������ֱ�������ڵ�O����һ��ON������OA�ϣ���һ��OM��OC����ֱ��AB���Ϸ���
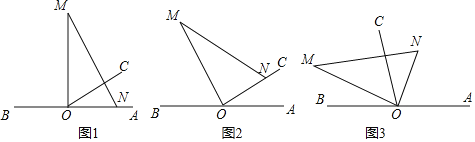
��1����ͼ1�е����ǰ��Ƶ�O��ÿ��5�����ٶ�����ʱ�뷽����תһ�ܣ���ͼ2������t���ON����OC���ϣ���t�����루ֱ��д�������
��2���ڣ�1���������£������ǰ����ת����ͬʱ����OCҲ��O����ÿ��10�����ٶ�����ʱ�뷽����תһ�ܣ���OCת��9��ʱ�����MOC�Ķ�����
��3���ڣ�2���������£����Ǽ����˶�������ʱ����MOC��35������˵�����ɣ�
���𰸡���1��6����2����MON��45�㣻��3�����Ǽ����˶�11���25ʱ����MOC��35�㣮
��������
��1�����ݣ����Ƕȣ��ٶ�![]() ʱ�䡱���м��㣬�������ʱ�䣻
ʱ�䡱���м��㣬�������ʱ�䣻
��2����t��9ʱ������á�AOC�͡�AON��ͨ������ǵIJ����ô𰸣�
��3�����췽����⼴�ɣ�ע���������.
��1��������5t��30�����t��6��
�ʴ�Ϊ6��
��2����t��9ʱ����AOC��30��+9��10�㣽120�㣬��AON��120��+9��5�㣽165�㣬
���ʱ��MON����AOC����AOM��165�㩁120�㣽45�㣮
��3��������˶�t��ʱ����MOC��35�㣮
�����⣺120��+5t����30��+10t����35���30��+10t����120��+5t����35��
���t��11��25��
�����Ǽ����˶�11���25ʱ����MOC��35�㣮


 â���̸����������������ϵ�д�
â���̸����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
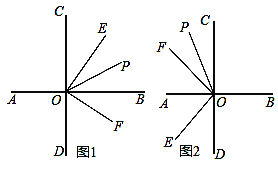
����Ŀ����ֱ֪��CD��AB�ڵ�O����EOF��90�㣬����OPƽ�֡�COF��
��1����ͼ1����EOF��ֱ��CD���Ҳࣺ
������COE��30�㣬���BOF�͡�POE�Ķ�����
�����жϡ�POE���BOP֮�����������������ϵ����˵�����ɣ�
��2����ͼ2����EOF��ֱ��CD����࣬�ҵ�E�ڵ�F���·���
����ֱ��д����POE���BOP֮���������ϵ��
����ֱ��д����POE���DOP֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ��LED��������ͨ�׳���ڣ�������������±������̳�����LED��������ͨ�׳���ڹ�300����LED���ݰ���۽������ۣ�����ͨ�׳���ڰ���۴�������ۣ��������������ݺ���Ի���3200Ԫ��
��1������̳�����LED��������ͨ�׳���ݵ������ֱ�Ϊ���ٸ���
��2�����ڴ����ڼ��������ܿ콫���ֵ��������꣬�����̳��ƻ��ٴι������ֵ���120�������ڲ����۵�����������꣬���������������ݵĻ����������ܽ����۵�28����������LED���ݶ��ٸ���
LED���� | ��ͨ�׳���� | |
���ۣ�Ԫ�� | 45 | 25 |
��ۣ�Ԫ�� | 60 | 30 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ڳ���һ�����������������¶Ȳ���ʱ���������������ѹp��kPa�����������V��m3���ķ�������������ͼ����ͼ��ʾ��

��1��д����һ�����ı���ʽ��
��2�����������Ϊ1 m3ʱ����ѹ�Ƕ��٣�
��3���������ڵ���ѹ����140 kPaʱ������ը��Ϊ�˰�ȫ��������������Ӧ��С�ڶ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ǽס�������ͬһ�ص������·����ʱ��仯��ͼ��

��1�����������У� ���Ա����� ���������
��2�����ٶ� �ҵ��ٶȣ���<��=����>����
��3��·��Ϊ150kmʱ������ʻ�� Сʱ������ʻ�� Сʱ��
��4���ױ��������� Сʱ����9ʱ�� ����ǰ�档
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ʽ![]() ...��������������
...��������������![]()
![]()
![]() �Դ����ƣ���
�Դ����ƣ���![]() ��ֵΪ�� ��
��ֵΪ�� ��
A.-1009B.-1008C.-2017D.-2018
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
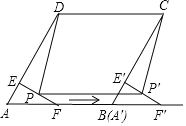
����Ŀ����ͼ��������ABCD�У���A��60����AD��8��F��AB���е㣬����F��FE��AD������ΪE������AEF�ص�A����B�ķ���ƽ�ƣ��õ���A��E��F����
��1����EF�ij���
��2����P��P���ֱ���EF��E��F�����е㣬����A�����B�غ�ʱ����֤�ı���PP��CD��ƽ���ı��Σ�������ı���PP��CD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��AB��BC��CD��BC������ֱ�ΪB��C��AB=BC��EΪBC���е�����AE��BD��F����CD=4cm����AB�ij���Ϊ��������

A. 4cm B. 8cm C. 9cm D. 10cm
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com