
【题目】已知整式![]() ...满足下列条件:
...满足下列条件:![]()
![]()
![]() 以此类推,则
以此类推,则![]() 的值为( )
的值为( )
A.-1009B.-1008C.-2017D.-2018
科目:初中数学 来源: 题型:
【题目】计算:
(1)+3+(-5)
(2)-89-11
(3)(﹣5.5)+(﹣3.2)﹣(﹣2.5)﹣4.8
(4)17﹣(﹣8)×(﹣2)+4×(﹣3)
(5)(-32![]() )-[5
)-[5![]() -(+3
-(+3![]() )+(-5
)+(-5![]() )+(-2
)+(-2![]() )]
)]
(6)(![]() )×(﹣12)
)×(﹣12)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】花果山是旅游胜地,据统计2014年9月30日花果山旅游人数为2万人, 十· 一黄金周期间,花果山7天中每天旅游人数的变化情况如下表(正数表示比9月30日多的人数,负数表示比9月30日少的人数):
![]()
(1)请判断7天内游客人数量最多和最少的各是哪一天?它们相差多少万人?
(2)求这7天去花果山旅游的总人数.
(3)如果去花果山旅游平均每人消费300元,求风景区在此7天内的总收入.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=3 cm,动点M自点A出发沿AB方向以1 cm/s的速度运动,同时点N自D点出发沿折线DC—CB以2 cm/s的速度运动,到达点B时运动同时停止,设△AMN的面积为y(单位:cm2),运动时间为x(单位:s),则下列图象中能大致反映y与x之间函数关系的是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角项点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
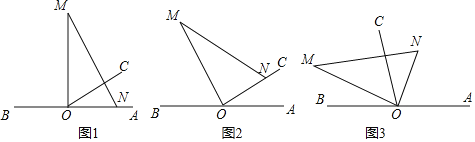
(1)将图1中的三角板绕点O以每秒5°的速度沿逆时针方向旋转一周.如图2,经过t秒后,ON落在OC边上,则t= 秒(直接写结果).
(2)在(1)的条件下,若三角板继续转动,同时射线OC也绕O点以每秒10°的速度沿逆时针方向旋转一周,当OC转动9秒时,求∠MOC的度数.
(3)在(2)的条件下,它们继续运动多少秒时,∠MOC=35°?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
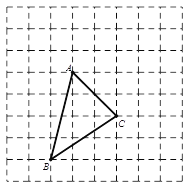
【题目】如图,在由边长为1的小正方形组成的网格图中有一个格点三角形ABC.(注:顶点均在网格线交点处的三角形称为格点三角形)
(1)请直接写出sin∠ABC的值: ;
(2)请在图中画格点三角形DEF,使得△DEF∽△ABC,且相似比为2∶1;
(3)请在图中确定格点M,使得△BCM的面积为6.如果符合题意的格点M不止一个,请分别用M1、M2、M3…表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种西装和领带,西装每套定价200元,领带每条定价40元.国庆节期间商场决定开展促销活动,活动期间向客户提供两种优惠方案:
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x![]() .
.
(1)若该客户按方案一购买,需付款多少元(用含x的式子表示)?若该客户按方案二购买,需付款多少元(用含x的式子表示)?
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算;
,通过计算说明此时按哪种方案购买较为合算;
(3)当![]() 时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,开口向上的抛物线与![]() 轴交于
轴交于![]() 两点,
两点, ![]() 为抛物线的顶点,
为抛物线的顶点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() . 若
. 若![]() 的长分别是方程
的长分别是方程![]() 的两根,且
的两根,且![]()
(1)求抛物线对应的二次函数解析式和点![]() 的坐标。
的坐标。
(2)若点M为x轴正半轴上一个动点,N为线段AC上的一个动点,连接MN、CM,是否存在这样的点M,使△AMN为直角三角形和△CMN为等腰三角形同时成立,如果存在,请求出所有符合条件的点M的坐标,如果不存在,请说明理由。
(3如图2,过点![]() 任作直线
任作直线![]() 交线段
交线段![]() 于点
于点![]() 求
求![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,请直接写出
,请直接写出![]() 的最大值.
的最大值.

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,先阅读再解决后面的问题:
原题:如图1,点E,F分别在正方形ABCD的边BC,CD上,![]() ,连接EF,求证:EF=BE+DF.
,连接EF,求证:EF=BE+DF.
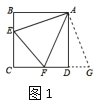
解题由于AB=AD,我们可以延长CD到点G,使DG=BE,易得![]() ,可证
,可证![]() .再证明
.再证明![]() ,得EF=FG=DG+FD=BE+DF.
,得EF=FG=DG+FD=BE+DF.
问题(1):如图2,在四边形ABCD中,AB=AD,![]() ,E,F分别是边BC,CD上的点,且
,E,F分别是边BC,CD上的点,且![]() ,求证:EF=BE+FD;
,求证:EF=BE+FD;

问题(2):如图3,在四边形ABCD中,![]() ,
,![]() ,AB=AD=1,点E,F分别在四边形ABCD的边BC,CD上的点,且
,AB=AD=1,点E,F分别在四边形ABCD的边BC,CD上的点,且![]() ,求此时
,求此时![]() 的周长
的周长

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com