
【题目】通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,先阅读再解决后面的问题:
原题:如图1,点E,F分别在正方形ABCD的边BC,CD上,![]() ,连接EF,求证:EF=BE+DF.
,连接EF,求证:EF=BE+DF.
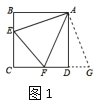
解题由于AB=AD,我们可以延长CD到点G,使DG=BE,易得![]() ,可证
,可证![]() .再证明
.再证明![]() ,得EF=FG=DG+FD=BE+DF.
,得EF=FG=DG+FD=BE+DF.
问题(1):如图2,在四边形ABCD中,AB=AD,![]() ,E,F分别是边BC,CD上的点,且
,E,F分别是边BC,CD上的点,且![]() ,求证:EF=BE+FD;
,求证:EF=BE+FD;

问题(2):如图3,在四边形ABCD中,![]() ,
,![]() ,AB=AD=1,点E,F分别在四边形ABCD的边BC,CD上的点,且
,AB=AD=1,点E,F分别在四边形ABCD的边BC,CD上的点,且![]() ,求此时
,求此时![]() 的周长
的周长

【答案】(1)![]() ,见解析;(2)
,见解析;(2)![]() 周长为
周长为![]() .
.
【解析】
(1)在CD的延长线上截取DG=BE,连接AG,证出△ABE≌△ADG,根据全等三角形的性质得出BE=DG,再证明△AEF≌△AGF,得EF=FG,即可得出答案;
(2)连接AC,证明△ABC≌△ADC(SSS).得∠DAC=∠BAC,同理由(1)得EF=BE+DF,可计算△CEF的周长.
证明:(1)在CD的延长线上截取DG=BE,连接AG,如图2,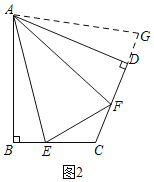
∵∠ADF=90°,∠ADF+∠ADG=180°,
∴∠ADG=90°,
∵∠B=90°,
∴∠B=∠ADG=90°,
∵BE=DG,AB=AD,
∴△ABE≌△ADG(SAS),
∴∠BAE=∠DAG,AG=AE,
∴∠EAG=∠EAD+∠DAG=∠EAD+∠ABE=∠BAD,
∵∠EAF=![]() ∠BAD,
∠BAD,
∵∠EAG=![]() ∠EAG=
∠EAG=![]() (∠EAF+∠FAG),
(∠EAF+∠FAG),
∴∠EAF=∠FAG,
又∵AF=AF,AE=AG,
∴△AEF≌△AFG(SAS),
∴EF=FG=DF+DG=EB+DF;
(2)解:连接AC,如图3,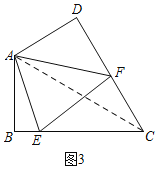
∵AB=AD,BC=CD,AC=AC,
∴△ABC≌△ADC(SSS).
∴∠DAC=∠BAC,
∴∠BAC=![]() ∠BAD=60°,
∠BAD=60°,
∵∠B=90°,AB=1,
∴在Rt△ABC中,AC=2,BC=![]() =
=![]() =
=![]() ,
,
由(1)得EF=BE+DF,
∴△CEF的周长=CE+CF+EF=2BC=2![]() .
.


科目:初中数学 来源: 题型:
【题目】为了丰富少年儿童的业余生活,某社区要在如图所示AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB⊥BC,CD⊥BC,垂足分别为B、C,AB=BC,E为BC的中点,且AE⊥BD于F,若CD=4cm,则AB的长度为( )

A. 4cm B. 8cm C. 9cm D. 10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB=![]() (
(![]() 为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足CQ=2AQ,CP=2BP.
为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足CQ=2AQ,CP=2BP.
(1)如图,当点C恰好在线段AB中点时,则PQ=_______(用含![]() 的代数式表示);
的代数式表示);
(2)若点C为直线AB上任一点,则PQ长度是否为常数?若是,请求出这个常数;若不是,请说明理由;
(3)若点C在点A左侧,同时点P在线段AB上(不与端点重合),请判断2AP+CQ-2PQ与1的大小关系,并说明理由。
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.则结论:①BE=EC;②∠EDC=∠ECD;③∠B=∠BDE;④△ABC∽△ACD;⑤△DEC是等边三角形.其中正确的结论有( )
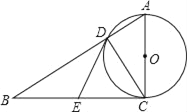
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
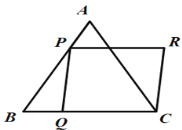
【题目】如图,等边△ABC边长为4,点P,Q分别是AB,BC边上的动点,且AP =BQ= x,作□PQCR,则用含x的代数式表示□PQCR的面积为______;当PC∥AR时, x =____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE,F为AE上一点,且∠BFE=∠C.
(1)求证: ![]() ;
;
(2)若AB=4,∠BAE=30°,求AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com