练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平行四边形ABCD中，过点B作BE⊥CD，垂足为E，连结AE，F为AE上一点，且∠BFE=∠C.

    （1）求证： ；

    （2）若AB=4，∠BAE=30°，求AE的长.

    【答案】(1)见解析；（2）

    【解析】试题分析：（1）可通过证明∠BAF=∠AED，∠AFB=∠D，证得△ABF∽△EAD；

    （2）先证出∠ABE=90°，再运用三角函数即可求出AE.

    试题解析：（1）∵四边形ABCD是平行四边形

    ∴AD//BC，

    ∴∠C+∠ADE=180°

    ∵BFE=∠C，

    ∴∠AFB=∠EDA

    又∵AB//DC

    ∴∠BAE=∠AED

    ∴.

    （2）∵AB//CD，BE⊥CD，

    ∴∠ABE=90°，

    又∵AB=4，∠BAE=30°

    设AE=x，则

    由勾股定理得

    解得.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】通过类比联想，引申拓展研究典型题目，可达到解一题知一类的目的.下面是一个案例，先阅读再解决后面的问题：

    原题：如图1，点E，F分别在正方形ABCD的边BC，CD上，，连接EF，求证：EF=BE+DF.

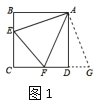
    解题由于AB=AD，我们可以延长CD到点G，使DG=BE，易得，可证.再证明，得EF=FG=DG+FD=BE+DF.

    问题（1）：如图2，在四边形ABCD中，AB=AD，，E，F分别是边BC，CD上的点，且，求证：EF=BE+FD；

    问题（2）：如图3，在四边形ABCD中，，，AB=AD=1，点E，F分别在四边形ABCD的边BC，CD上的点，且，求此时的周长

    查看答案和解析>>

    科目：初中数学 来源： 题型：

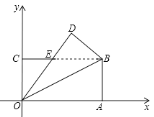
    【题目】如图，矩形OABC的顶点与坐标原点O重合，将△OAB沿对角线OB所在的直线翻折，点A落在点D处，OD与BC相交于点E，已知OA=8，AB=4

    （1）求证：△OBE是等腰三角形；

    （2）求E点的坐标；

    （3）坐标平面内是否存在一点P，使得以B，D，E，P为顶点的四边形是平行四边形？若存在，请直接写出P点坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形中，对角线的垂直平分线分别交、、于点、、，连接和.

    （1）求证：四边形为菱形.

    （2）若，，求菱形的周长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图，在矩形ABCD中.点O在边AB上，∠AOC=∠BOD.求证：AO=OB.

    （2）如图，AB是的直径，PA与相切于点A，OP与相交于点C，连接CB，∠OPA=40°，求∠ABC的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在正方形ABCD中，动点E，F分别从D，C两点同时出发，以相同的速度在直线DC，CB上移动.

    （1）如图1，当点E在边DC上自D向C移动，同时点F在边CB上自C向B移动时，连接AE和DF交于点P，请你写出AE与DF的数量关系和位置关系，并说明理；

    （2）如图2，当E，F分别在边CD，BC的延长线上移动时，连接AE，DF，（1）中的结论还成立吗？（请你直接回答“是”或“否”，不需证明）；连接AC，求△ACE为等腰三角形时CE：CD的值；

    （3）如图3，当E，F分别在直线DC，CB上移动时，连接AE和DF交于点P，由于点E，F的移动，使得点P也随之运动，请你画出点P运动路径的草图.若AD=2，试求出线段CP的最大值.

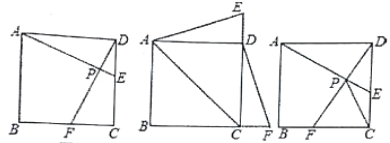
    图1 图2 图3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB与CD相交于点O，OE平分∠AOD，OF平分∠BOD.

    (1)若∠AOC＝70°，求∠DOE和∠EOF的度数；

    (2)请写出图中∠AOD的补角和∠AOE的余角．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数轴上A，B，C三点对应的数a，b，c满足(a+40)2+|b+10|＝0，B为线段AC的中点.

    (1)直接写出A，B，C对应的数a，b，c的值.

    (2)如图1，点D表示的数为10，点P，Q分别从A，D同时出发匀速相向运动，点P的速度为6个单位/秒，点Q的速度为1个单位/秒.当点P运动到C后迅速以原速返回到A又折返向C点运动；点Q运动至B点后停止运动，同时P点也停止运动.求在此运动过程中P，Q两点相遇点在数轴上对应的数.

    (3)如图2，M，N为A，C之间两点(点M在N左边，且它们不与A，C重合)，E，F分别为AN，CM的中点，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在如图的2016年6月份的日历表中，任意框出表中竖列上三个相邻的数，这三个数的和不可能是(　 　)

    A. 27 B. 51 C. 69 D. 72

    查看答案和解析>>

    同步练习册答案