
【题目】如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD.
(1)若∠AOC=70°,求∠DOE和∠EOF的度数;
(2)请写出图中∠AOD的补角和∠AOE的余角.

【答案】(1) 90°;(2)∠AOD的补角:∠AOC和∠BOD;∠AOE的余角:∠DOF和∠BOF.
【解析】
(1)根据邻补角的定义求出∠AOD,再根据角平分线的定义求解即可得到∠DOE,根据对顶角相等可得∠BOD=∠AOC,再根据角平分线的定义∠DOF,然后根据∠EOF=∠DOE+∠DOF计算即可得解;
(2)根据邻补角的定义和互补的角的定义解答即可;根据互余的角的定义解答即可.
(1)因为∠AOC=70°,
所以∠AOD=180°-∠AOC=110°,
所以∠BOD=180°-∠AOD=70°.
又因为OE平分∠AOD,所以∠DOE=![]() ∠AOD=55°,
∠AOD=55°,
又因为OF平分∠BOD,所以∠DOF=![]() ∠BOD=35°.
∠BOD=35°.
所以∠EOF=∠DOE+∠DOF=90°.
(2)∠AOD的补角:∠AOC和∠BOD;
∠AOE的余角:∠DOF和∠BOF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】从共享单车,共享汽车等共享出行到共享充电宝,共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速普及应用,越来越多的企业与个人成为参与者与受益者.根据国家信息中心发布的《中国分享经济发展报告2017》显示,2016年我国共享经济市场交易额约为34520亿元,比上年增长103%;超6亿人参与共享经济活动,比上年增加约1亿人.
如图是源于该报告中的中国共享经济重点领域市场规模统计图: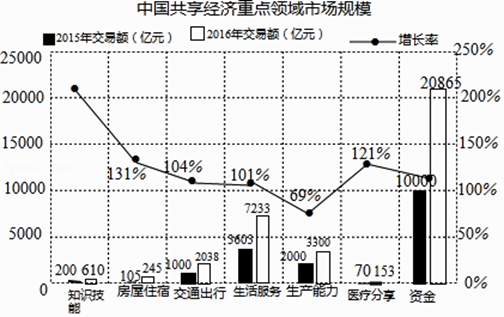
(1)请根据统计图解答下列问题:
①图中涉及的七个重点领域中,2016年交易额的中位数是亿元.
②请分别计算图中的“知识技能”和“资金”两个重点领域从2015年到2016年交易额的增长率(精确到1%),并就这两个重点领域中的一个分别从交易额和增长率两个方面,谈谈你的认识.
(2)小宇和小强分别对共享经济中的“共享出行”和“共享知识”最感兴趣,他们上网查阅了相关资料,顺便收集到四个共享经济领域的图标,并将其制成编号为A,B,C,D的四张卡片(除编号和内容外,其余完全相同)他们将这四张卡片背面朝上,洗匀放好,从中随机抽取一张(不放回),再从中随机抽取一张,请用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率(这四张卡片分别用它们的编号A,B,C,D表示)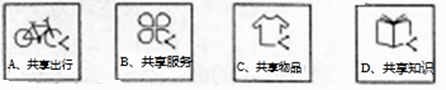
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y= ![]() x2+bx+c与x轴交于A(﹣1,0),B(2,0)两点,与y轴交于点C.
x2+bx+c与x轴交于A(﹣1,0),B(2,0)两点,与y轴交于点C.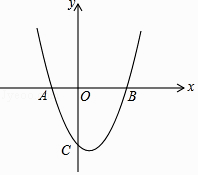
(1)求该抛物线的解析式;
(2)直线y=﹣x+n与该抛物线在第四象限内交于点D,与线段BC交于点E,与x轴交于点F,且BE=4EC.
①求n的值;
②连接AC,CD,线段AC与线段DF交于点G,△AGF与△CGD是否全等?请说明理由;
(3)直线y=m(m>0)与该抛物线的交点为M,N(点M在点N的左侧),点 M关于y轴的对称点为点M',点H的坐标为(1,0).若四边形OM'NH的面积为 ![]() .求点H到OM'的距离d的值.
.求点H到OM'的距离d的值.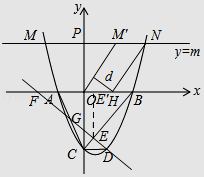
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉嘉在电脑上设计了一个有理数的运算程序:输入a,加*键,再输入b,得到运算a*b=(a2-b2)÷(a-b) .
(1)求(-2)*![]() *
* ![]() 的值;
的值;
(2)琪琪在运用此程序计算时,屏幕上显示“该程序无法操作”,请你运用所学的数学知识猜想一下,琪琪在输入数据时,可能出现什么情况?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两同心圆的圆心为O,大圆的弦AB与小圆相切于点P,已知两圆的半径分别为2和1,用阴影部分围成一个圆锥(OA与OB重合),则该圆锥的底面半径是( ) 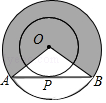
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:
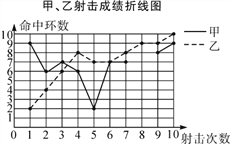
甲、乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中10环的次数 | |
甲 | 7 | |||
乙 | 1 |
(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁将胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料: 如图1,圆的概念:在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上,圆心在P(a,b),半径为r的圆的方程可以写为:(x﹣a)2+(y﹣b)2=r2 , 如:圆心在P(2,﹣1),半径为5的圆方程为:(x﹣2)2+(y+1)2=25
(1)填空: ①以A(3,0)为圆心,1为半径的圆的方程为;
②以B(﹣1,﹣2)为圆心, ![]() 为半径的圆的方程为 .
为半径的圆的方程为 .
(2)根据以上材料解决下列问题: 如图2,以B(﹣6,0)为圆心的圆与y轴相切于原点,C是⊙B上一点,连接OC,作BD⊥OC垂足为D,延长BD交y轴于点E,已知sin∠AOC= ![]() .
.
①连接EC,证明EC是⊙B的切线;
②在BE上是否存在一点P,使PB=PC=PE=PO?若存在,求P点坐标,并写出以P为圆心,以PB为半径的⊙P的方程;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,求AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com