
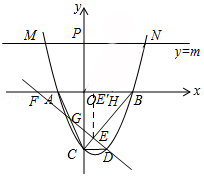
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������y= ![]() x2+bx+c��x�ύ��A����1��0����B��2��0�����㣬��y�ύ�ڵ�C��
x2+bx+c��x�ύ��A����1��0����B��2��0�����㣬��y�ύ�ڵ�C��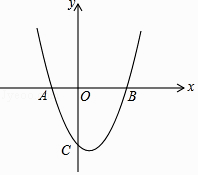
��1����������ߵĽ���ʽ��
��2��ֱ��y=��x+n����������ڵ��������ڽ��ڵ�D�����߶�BC���ڵ�E����x�ύ�ڵ�F����BE=4EC��
����n��ֵ��
������AC��CD���߶�AC���߶�DF���ڵ�G����AGF���CGD�Ƿ�ȫ�ȣ���˵�����ɣ�
��3��ֱ��y=m��m��0����������ߵĽ���ΪM��N����M�ڵ�N����ࣩ���� M����y��ĶԳƵ�Ϊ��M'����H������Ϊ��1��0�������ı���OM'NH�����Ϊ ![]() �����H��OM'�ľ���d��ֵ��
�����H��OM'�ľ���d��ֵ��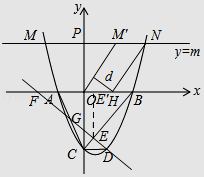
���𰸡�
��1��
�⣺��������y= ![]() x2+bx+c��x�ύ��A����1��0����B��2��0�����㣬
x2+bx+c��x�ύ��A����1��0����B��2��0�����㣬
�� 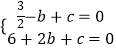 �����
����� 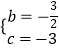 ��
��
��������ߵĽ���ʽy= ![]() x2��
x2�� ![]() x��3��
x��3��
��2��
�⣺����ͼ������E��EE'��x����E'����EE'��OC��
�� ![]() =
= ![]() ��
��
��BE=4EC��
��BE'=4OE'��
���E��������x��y������OE'=x��BE'=4x��
��B��2��0����
��OB=2����x+4x=2��
��x= ![]() ��
��
��������y= ![]() x2��
x2�� ![]() x��3��y�ύ�ڵ�C��
x��3��y�ύ�ڵ�C��
��C��0����3����
��ֱ��BC�Ľ���ʽΪy=kx+b'��
��B��2��0����C��0����3����
�� ![]() �����
����� 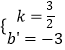 ��
��
��ֱ��BC�Ľ���ʽΪy= ![]() x��3��
x��3��
��x= ![]() ʱ��y=��
ʱ��y=�� ![]() ��
��
��E�� ![]() ����
���� ![]() ����
����
��E���������ֱ��y=��x+n���ɵé� ![]() +n=��
+n=�� ![]() ��
��
���n=��2��
�ڡ�AGF���CGDȫ�ȣ��������£�
��ֱ��EF�Ľ���ʽΪy=��x��2��
�൱y=0ʱ��x=��2��
��F����2��0����OF=2��
��A����1��0����
��OA=1��
��AF=2��1=1��
�� 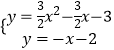 ���
��� 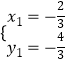 ��
�� ![]() ��
��
�ߵ�D�ڵ������ޣ�
���D��������1����3����
�ߵ�C������Ϊ��0����3����
��CD��x�ᣬCD=1��
���AFG=��CDG����FAG=��DCG��
���AGF�ա�CGD��
��3��
�⣺�������ߵĶԳ���Ϊx=�� ![]() =
= ![]() ��ֱ��y=m��m��0����������ߵĽ���ΪM��N��
��ֱ��y=m��m��0����������ߵĽ���ΪM��N��
���M��N����ֱ��x= ![]() �Գƣ�
�Գƣ�
��N��t��m������M��1��t��m����
�ߵ� M����y��ĶԳƵ�Ϊ��M'��
��M'��t��1��m����
���M'��ֱ��y=m�ϣ�
��M'N��x�ᣬ
��M'N=t����t��1��=1��
��H��1��0����
��OH=1=M'N��
���ı���OM'NH��ƽ���ı��Σ�
��ֱ��y=m��y�ύ�ڵ�P��
���ı���OM'NH�����Ϊ ![]() ��
��
��OH��OP=1��m= ![]() ����m=
����m= ![]() ��
��
��OP= ![]() ��
��
�� ![]() x2��
x2�� ![]() x��3=
x��3= ![]() ʱ�����x1=��
ʱ�����x1=�� ![]() ��x2=
��x2= ![]() ��
��
���M���������� ![]() ��
�� ![]() ����
����
��M'�� ![]() ��
�� ![]() ������PM'=
������PM'= ![]() ��
��
��Rt��OPM'��OM'= ![]() =
= ![]() ��
��
���ı���OM'NH�����Ϊ ![]() ��
��
��OM'��d= ![]() ��
��
��d= ![]() ��
��
����������1������������y= ![]() x2+bx+c��x�ύ��A����1��0����B��2��0�����㣬�ɵ������ߵĽ���ʽ����2���ٹ���E��EE'��x����E'����EE'��OC������ƽ���߷��߶γɱ����������ɵ�BE'=4OE'�����E������Ϊ��x��y������OE'=x��BE'=4x������OB=2���ɵ�x=
x2+bx+c��x�ύ��A����1��0����B��2��0�����㣬�ɵ������ߵĽ���ʽ����2���ٹ���E��EE'��x����E'����EE'��OC������ƽ���߷��߶γɱ����������ɵ�BE'=4OE'�����E������Ϊ��x��y������OE'=x��BE'=4x������OB=2���ɵ�x= ![]() ���ٸ���ֱ��BC�Ľ���ʽΪy=
���ٸ���ֱ��BC�Ľ���ʽΪy= ![]() x��3�����ɵõ�E��
x��3�����ɵõ�E�� ![]() ����
���� ![]() ������E���������ֱ��y=��x+n���ɵ�n��ֵ���ڸ���F����2��0����A����1��0�����ɵ�AF=1���ٸ��ݵ�D������Ϊ��1����3������C������Ϊ��0����3�����ɵ�CD��x�ᣬCD=1���ٸ��ݡ�AFG=��CDG����FAG=��DCG�������ж���AGF�ա�CGD����3��������ԳƵ����ʵó�OH=1=M'N�������ж��ı���OM'NH��ƽ���ı��Σ��ٸ����ı���OM'NH�����Ϊ
������E���������ֱ��y=��x+n���ɵ�n��ֵ���ڸ���F����2��0����A����1��0�����ɵ�AF=1���ٸ��ݵ�D������Ϊ��1����3������C������Ϊ��0����3�����ɵ�CD��x�ᣬCD=1���ٸ��ݡ�AFG=��CDG����FAG=��DCG�������ж���AGF�ա�CGD����3��������ԳƵ����ʵó�OH=1=M'N�������ж��ı���OM'NH��ƽ���ı��Σ��ٸ����ı���OM'NH�����Ϊ ![]() �����OP=
�����OP= ![]() ���ٸ��ݵ�M������Ϊ����
���ٸ��ݵ�M������Ϊ���� ![]() ��
�� ![]() �����õ�PM'=
�����õ�PM'= ![]() ��Rt��OPM'�У����ù��ɶ����ɵ�OM'=
��Rt��OPM'�У����ù��ɶ����ɵ�OM'= ![]() ��������OM'��d=
��������OM'��d= ![]() �����ɵõ�d=
�����ɵõ�d= ![]() ��
��
�����㾫����������Ŀ����֪���������ö��κ��������ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��


 ��ĩ�óɼ�ϵ�д�
��ĩ�óɼ�ϵ�д� 99��1������ĩ��ѵ��ϵ�д�
99��1������ĩ��ѵ��ϵ�д� ��ǿ��У��ĩ���100��ϵ�д�
��ǿ��У��ĩ���100��ϵ�д� �óɼ�1��1��ĩ���100��ϵ�д�
�óɼ�1��1��ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����Rt��AOB�У���A=90������AOB=60����OB=![]() ����AOB��ƽ����OC��AB��C����O������OB��ֱ��ֱ��ON������P�ӵ�B����������BC��CO��ÿ��1����λ���ȵ��ٶ����յ�O�˶����˶�ʱ��Ϊt�룬ͬʱ����Q�ӵ�C����������CO��ON����ͬ���ٶ��˶�������P�����OʱP��Qͬʱֹͣ�˶���
����AOB��ƽ����OC��AB��C����O������OB��ֱ��ֱ��ON������P�ӵ�B����������BC��CO��ÿ��1����λ���ȵ��ٶ����յ�O�˶����˶�ʱ��Ϊt�룬ͬʱ����Q�ӵ�C����������CO��ON����ͬ���ٶ��˶�������P�����OʱP��Qͬʱֹͣ�˶���
��1����OC��BC�ij���
��2������CPQ�����ΪS����S��t�ĺ�����ϵʽ��
��3����P��OC��Q��ON���˶�ʱ����ͼ��2������PQ��OA���ڵ�M����tΪ��ֵʱ����OPMΪ���������Σ������������������tֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ڿ������п�������һ���������Ļ�������⣺
���㣺![]()
�����֣������ʽ��ӳ����ǰ�������ֵĺͣ�����������֮�������ij�ֹ�ϵ���������ֹ�ϵ����˳���ؽ��������⡣
��1��ǰ��������֮�������ʲô��ϵ��
��2���ȼ����IJ��ֱȽϼ�㣿�������Ƚϼ����Dz��֡�
��3�����ã�1���еĹ�ϵ��ֱ��д����һ���ֵĽ����
��4���������Ϸ��������ԭʽ�Ľ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��̽��֤����
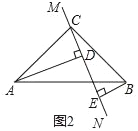
�ڡ�ABC�У���ACB=90�㣬AC=BC��ֱ��MN������C����AD��MN�ڵ�D��BE��MN�ڵ�E����ֱ��MN�Ƶ�C��ת��ͼ1��λ��ʱ����֤��DE=AD+BE��
��2������̽����
��ֱ��MN�Ƶ�C��ת��ͼ2��λ��ʱ����1���еĽ����Ƿ�����������������DE��AD��BEӦ����Ĺ�ϵ��_____��
��3��������⣺
��ֱ��MN�Ƶ�C��ת��ͼ3��λ��ʱ����BE=8��AD=2����ֱ��д��DE�ij�Ϊ_____��

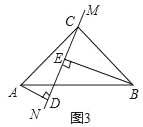
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ڡ�ABC�У�AB��17��AC��10��BC���ϵĸ�AD��8�����BC�ij�Ϊ( )
A. 21 B. 15 C. 9 D. 9��21
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������·��ͨ�����������涨��С�����ڳǽ�����ʻ�ٶȲ��ó���70ǧ��/Сʱ����ͼ��һ��С������һ�����н�·��ֱ����ʻ��ijһʱ�̸պ���ʻ��·��Գ��ټ����A��ǰ��30��B��������2����С����C�복�ټ����A�����Ϊ50�ף�����С������������
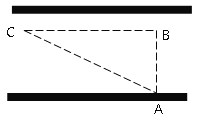
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˸��ø��ƺ�����ˮ�ʣ����۹�˾��������10̨��ˮ�����豸![]() ����A��B�����ͺŵ��豸������ÿ̨�ļ۸��´�����ˮ�����±��������飺����һ̨A���豸�ȹ���һ̨B���豸��2��Ԫ������2̨A���豸�ȹ���3̨B���豸��6��Ԫ��
����A��B�����ͺŵ��豸������ÿ̨�ļ۸��´�����ˮ�����±��������飺����һ̨A���豸�ȹ���һ̨B���豸��2��Ԫ������2̨A���豸�ȹ���3̨B���豸��6��Ԫ��
A�� | B�� | |
�۸� | a | b |
������ˮ�� | 240 | 200 |
![]() ��a��b��ֵ��
��a��b��ֵ��
![]() ���۹�˾��Ԥ�㹺����ˮ�����豸���ʽ���105��Ԫ������Ϊ�ù�˾���ļ��ֹ�����
���۹�˾��Ԥ�㹺����ˮ�����豸���ʽ���105��Ԫ������Ϊ�ù�˾���ļ��ֹ�����
![]() ��
��![]() �������£���ÿ��Ҫ������ˮ��������2040�֣�Ϊ�˽�Լ�ʽ�����Ϊ���۹�˾���һ����ʡǮ�Ĺ�����
�������£���ÿ��Ҫ������ˮ��������2040�֣�Ϊ�˽�Լ�ʽ�����Ϊ���۹�˾���һ����ʡǮ�Ĺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD�ཻ�ڵ�O��OEƽ�֡�AOD��OFƽ�֡�BOD.
(1)����AOC��70�㣬���DOE�͡�EOF�Ķ�����
(2)��д��ͼ�С�AOD�IJ��Ǻ͡�AOE����ǣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��÷����ѧΪ�˽����γ�ѡ������������Ա����μ������������������Ƽ�������������ѧ˼ά�������Ķ�д�������ĸ�ѡ����Ŀ��ѧ����ÿ���ޱ�һ�Σ����г������飬�����Ǹ����ռ������ݻ��ƵIJ�������ͳ��ͼ�������ͼ���ṩ����Ϣ�������������⣺
��1���˴ι�������______��ѧ��������ͳ��ͼ�����������������ֵ�Բ�Ľ���______�ȣ�
��2������������ͳ��ͼ����������
��3���ָ�У����800��ѧ�������μ����ĸ�ѡ����Ŀ��������������ж�����ѧ��ѡ�� ���Ƽ���������Ŀ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com