
【题目】阅读下列材料: 如图1,圆的概念:在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上,圆心在P(a,b),半径为r的圆的方程可以写为:(x﹣a)2+(y﹣b)2=r2 , 如:圆心在P(2,﹣1),半径为5的圆方程为:(x﹣2)2+(y+1)2=25
(1)填空: ①以A(3,0)为圆心,1为半径的圆的方程为;
②以B(﹣1,﹣2)为圆心, ![]() 为半径的圆的方程为 .
为半径的圆的方程为 .
(2)根据以上材料解决下列问题: 如图2,以B(﹣6,0)为圆心的圆与y轴相切于原点,C是⊙B上一点,连接OC,作BD⊥OC垂足为D,延长BD交y轴于点E,已知sin∠AOC= ![]() .
.
①连接EC,证明EC是⊙B的切线;
②在BE上是否存在一点P,使PB=PC=PE=PO?若存在,求P点坐标,并写出以P为圆心,以PB为半径的⊙P的方程;若不存在,说明理由.
【答案】
(1)(x﹣3)2+y2=1;(x+1)2+(y+2)2=3
(2)解:①证明:∵BD⊥OC,
∴CD=OD,
∴BE垂直平分OC,
∴EO=EC,
∴∠EOC=∠ECO,
∵BO=BC,
∴∠BOC=∠BCO,
∴∠EOC+∠BOC=∠ECO+∠BCO,
∴∠BOE=∠BCE=90°,
∴BC⊥CE,
∴EC是⊙B的切线;
②存在.
∵∠BOE=∠BCE=90°,
∴点C和点O偶在以BE为直径的圆上,
∴当P点为BE的中点时,满足PB=PC=PE=PO,
∵B点坐标为(﹣6,0),
∴OB=6,
∵∠AOC+∠DOE=90°,∠DOE+∠BEO=90°,
∴∠BEO=∠AOC,
∴sin∠BEO=sin∠AOC= ![]() ,
,
在Rt△BOE中,sin∠BEO= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BE=10,
∴OE= ![]() =8,
=8,
∴E点坐标为(0,8),
∴线段AB的中点P的坐标为(﹣3,4),PB=5,
∴以P(﹣3,4)为圆心,以5为半径的⊙P的方程为(x+3)2+(y﹣4)2=25.

【解析】(1)解:①以A(3,0)为圆心,1为半径的圆的方程为(x﹣3)2+y2=1; ②以B(﹣1,﹣2)为圆心, ![]() 为半径的圆的方程为(x+1)2+(y+2)2=3;
为半径的圆的方程为(x+1)2+(y+2)2=3;
故答案为(x﹣3)2+y2=1;(x+1)2+(y+2)2=3;
(1)根据阅读材料中的定义求解;(2)①根据垂径定理由BD⊥OC得到CD=OD,则BE垂直平分OC,再根据线段垂直平分线的性质得EO=EC,则∠EOC=∠ECO,加上∠BOC=∠BCO,易得∠BOE=∠BCE=90°,然后根据切线的判定定理得到EC是⊙B的切线;②由∠BOE=∠BCE=90°,根据圆周角定理得点C和点O偶在以BE为直径的圆上,即当P点为BE的中点时,满足PB=PC=PE=PO,利用同角的余角相等得∠BOE=∠AOC,则sin∠BOE=sin∠AOC= ![]() ,在Rt△BOE中,利用正弦的定义计算出BE=10,利用勾股定理计算出OE=8,则E点坐标为(0,8),于是得到线段AB的中点P的坐标为(﹣3,4),PB=5,然后写出以P(﹣3,4)为圆心,以5为半径的⊙P的方程.
,在Rt△BOE中,利用正弦的定义计算出BE=10,利用勾股定理计算出OE=8,则E点坐标为(0,8),于是得到线段AB的中点P的坐标为(﹣3,4),PB=5,然后写出以P(﹣3,4)为圆心,以5为半径的⊙P的方程.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
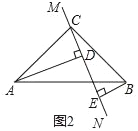
【题目】(1)探究证明:
在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E,当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE;
(2)发现探究:
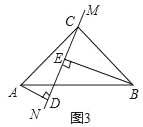
当直线MN绕点C旋转到图2的位置时,(1)中的结论是否成立,如果不成立,DE、AD、BE应满足的关系是_____.
(3)解决问题:
当直线MN绕点C旋转到图3的位置时,若BE=8,AD=2,请直接写出DE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD.
(1)若∠AOC=70°,求∠DOE和∠EOF的度数;
(2)请写出图中∠AOD的补角和∠AOE的余角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,点A、B、C、M、N都在格点上(不写作法)
(1)作△ABC关于直线MN对称的△A’B’C’:
(2)将△ABC向上平移两个单位得△A1B1C1,画出△A1B1C1;
(3)在直线MN上找一点P,使AP+CP的值最小.
(4)若网格中最小正方形的边长为1,直接写出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人两次同时在一家粮店购买大米,两次大米的价格分别为每千克a元和b元(a≠b).甲每次买100千克大米,乙每次买100元大米.
(1)用含a、b的代数式表示:甲两次购买大米共需付款 元,乙两次共购买 千克大米.若甲两次购买大米的平均单价为每千克Q1元,乙两次购买大米的平均单价为每千克Q2元.则:Q1= ;Q2= .
(2)若规定谁两次购粮的平均价格低,谁购粮的方式就更合理,请你判断比较甲、乙两人的购粮方式,哪一个更合理,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】梅岭中学为了解“课程选修”的情况,对报名参加“艺术欣赏”,“科技制作”,“数学思维”,“阅读写作”这四个选修项目的学生(每人限报一课)进行抽样调查,下面是根据收集的数据绘制的不完整的统计图,请根据图中提供的信息,解答下面的问题:
(1)此次共调查了______名学生,扇形统计图中“艺术欣赏”部分的圆心角是______度;
(2)请把这个条形统计图补充完整;
(3)现该校共有800名学生报名参加这四个选修项目,请你估计其中有多少名学生选修 “科技制作”项目.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段CB=6,点A在线段BC上,且CA=2,以AB为直径做半圆O,点D为半圆O上的动点,以CD为边向外作等边△CDE.
(1)发现:CD的最小值是 , 最大值是 , △CBD面积的最大值是 .
(2)思考:如图1,当线段CD所在直线与半圆O相切时,求弧BD的长. 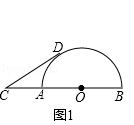
(3)探究:如图2,当线段CD与半圆O有两个公共点D,M时,若CM=DM,求等边△CDE面积. 
查看答案和解析>>
科目:初中数学 来源: 题型:
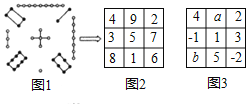
【题目】(阅读材料)“九宫图”源于我国古代夏禹时期的“洛书”![]() 图1所示
图1所示![]() ,是世界上最早的矩阵,又称“幻方”,用今天的数学符号翻译出来,“洛书”就是一个三阶“幻方”
,是世界上最早的矩阵,又称“幻方”,用今天的数学符号翻译出来,“洛书”就是一个三阶“幻方”![]() 图2所示
图2所示![]() .
.
(规律总结)观察图1、图2,根据“九宫图”中各数字之间的关系,我们可以总结出“幻方”需要满足的条件是______;若图3,是一个“幻方”,则![]() ______.
______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com