
【题目】已知:线段CB=6,点A在线段BC上,且CA=2,以AB为直径做半圆O,点D为半圆O上的动点,以CD为边向外作等边△CDE.
(1)发现:CD的最小值是 , 最大值是 , △CBD面积的最大值是 .
(2)思考:如图1,当线段CD所在直线与半圆O相切时,求弧BD的长. 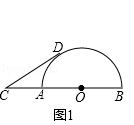
(3)探究:如图2,当线段CD与半圆O有两个公共点D,M时,若CM=DM,求等边△CDE面积. 
【答案】
(1)2;6;6
(2)解:连接OD,
∵线段CD所在直线与半圆O相切,
∴OD⊥CD,
∵OC=4,OD=2,
∴∠C=30°,
∴∠COD=60°,
∴∠BOD=120°,
∴弧BD的长为: ![]() =
= ![]() π
π
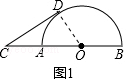
(3)解:∵CM=DM,
∴CD=2CM,
由切割线定理得,CMCD=CACB=12,
解得,CM= ![]() ,
,
则CD=2 ![]() ,
,
∴等边△CDE面积为: ![]() ×2
×2 ![]() ×2
×2 ![]() ×sin60°=6
×sin60°=6 ![]()
【解析】解:(1)发现:当点D与点A重合时,CD最小,CD的最小值是2, 当点D与点B重合时,CD最大,CD的最大值是6,
当OD⊥CB时,CD最小,△CBD的面积最大,最大值为: ![]() ×6×2=6,
×6×2=6,
故答案为:2;6;6;
发现:根据圆的性质、三角形的面积公式计算;
思考:连接OD,根据切线的性质得到OD⊥CD,根据直角三角形的性质求出∠C,得到∠BOD,根据弧长公式计算即可;
探究:根据切割线定理求出CD,根据等边三角形的面积公式计算即可.


科目:初中数学 来源: 题型:
【题目】阅读下列材料: 如图1,圆的概念:在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上,圆心在P(a,b),半径为r的圆的方程可以写为:(x﹣a)2+(y﹣b)2=r2 , 如:圆心在P(2,﹣1),半径为5的圆方程为:(x﹣2)2+(y+1)2=25
(1)填空: ①以A(3,0)为圆心,1为半径的圆的方程为;
②以B(﹣1,﹣2)为圆心, ![]() 为半径的圆的方程为 .
为半径的圆的方程为 .
(2)根据以上材料解决下列问题: 如图2,以B(﹣6,0)为圆心的圆与y轴相切于原点,C是⊙B上一点,连接OC,作BD⊥OC垂足为D,延长BD交y轴于点E,已知sin∠AOC= ![]() .
.
①连接EC,证明EC是⊙B的切线;
②在BE上是否存在一点P,使PB=PC=PE=PO?若存在,求P点坐标,并写出以P为圆心,以PB为半径的⊙P的方程;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台在它的娱乐性节目中每期抽出两名场外幸运观众,有一期甲、乙两人被抽为场外幸运观众,他们获得了一次抽奖的机会,在如图所示的翻奖牌的正面4个数字中任选一个,选中后翻开,可以得到该数字反面的奖品,第一个人选中的数字第二个人不能再选择了. 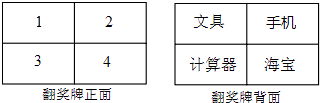
(1)如果甲先抽奖,那么甲获得“手机”的概率是多少?
(2)小亮同学说:甲先抽奖,乙后抽奖,甲、乙两人获得“手机”的概率不同,且甲获得“手机”的概率更大些.你同意小亮同学的说法吗?为什么?请用列表或画树状图分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.
(1)旋转中心是点 ,旋转角度是 度;
(2)若连结EF,则△AEF是 三角形;并证明;
(3)若四边形AECF的面积为25,DE=2,求AE的长.
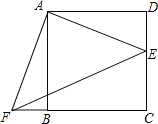
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧 ![]() 、
、 ![]() 是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )
是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )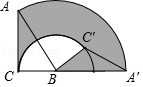
A.4π+2 ![]()
B.![]()
π﹣2 ![]()
C.![]()
π+2 ![]()
D.4π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△AOB中,将扇形COD按图1摆放,使扇形的半径OC、OD分别与OA、OB重合,OA=OB=2,OC=OD=1,固定等边△AOB不动,让扇形COD绕点O逆时针旋转,线段AC、BD也随之变化,设旋转角为α.(0<α≤360°) 
(1)当OC∥AB时,旋转角α=度;
(2)线段AC与BD有何数量关系,请仅就图2给出证明. 
(3)当A、C、D三点共线时,求BD的长.
(4)P是线段AB上任意一点,在扇形COD的旋转过程中,请直接写出线段PC的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
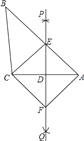
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com