
【题目】在等边△AOB中,将扇形COD按图1摆放,使扇形的半径OC、OD分别与OA、OB重合,OA=OB=2,OC=OD=1,固定等边△AOB不动,让扇形COD绕点O逆时针旋转,线段AC、BD也随之变化,设旋转角为α.(0<α≤360°) 
(1)当OC∥AB时,旋转角α=度;
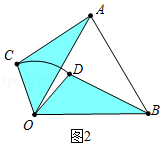
(2)线段AC与BD有何数量关系,请仅就图2给出证明. 
(3)当A、C、D三点共线时,求BD的长.
(4)P是线段AB上任意一点,在扇形COD的旋转过程中,请直接写出线段PC的最大值与最小值.
【答案】
(1)60或240
(2)解:结论:AC=BD,理由如下:
如图2中,
∵∠COD=∠AOB=60°,
∴∠COA=∠DOB,
在△AOC和△BOD中,
 ,
,
∴△AOC≌△BOD,
∴AC=BD
(3)解:①如图3中,当A、C、D共线时,作OH⊥AC于H.
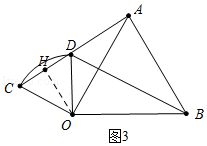
在Rt△COH中,∵OC=1,∠COH=30°,
∴CH=HD= ![]() ,OH=
,OH= ![]() ,
,
在Rt△AOH中,
AH= ![]() =
= ![]() ,
,
∴BD=AC=CH+AH= ![]() .
.
如图4中,当A、C、D共线时,作OH⊥AC于H.
易知AC=BD=AH﹣CH= ![]() ,
,
综上所述,当A、C、D三点共线时,BD的长为 ![]() 或
或 ![]()
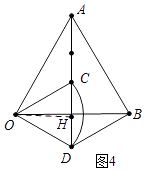
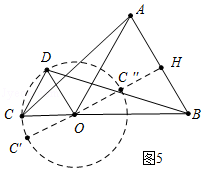
(4)解:如图5中,由题意,点C在以O为圆心,1为半径的⊙O上运动,过点O作OH⊥AB于H,直线OH交⊙O于C′、C″,线段CB的长即为PC的最大值,线段C″H的长即为PC的最小值.易知PC的最大值=3,PC的最小值= ![]() ﹣1.
﹣1.
【解析】解:(1)如图1中, 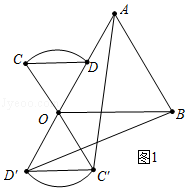
∵△ABC是等边三角形,
∴∠AOB=∠COD=60°,
∴当点D在线段AD和线段AD的延长线上时,OC∥AB,
此时旋转角α=60°或240°.
所以答案是60或240;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,点A、B、C、M、N都在格点上(不写作法)
(1)作△ABC关于直线MN对称的△A’B’C’:
(2)将△ABC向上平移两个单位得△A1B1C1,画出△A1B1C1;
(3)在直线MN上找一点P,使AP+CP的值最小.
(4)若网格中最小正方形的边长为1,直接写出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段CB=6,点A在线段BC上,且CA=2,以AB为直径做半圆O,点D为半圆O上的动点,以CD为边向外作等边△CDE.
(1)发现:CD的最小值是 , 最大值是 , △CBD面积的最大值是 .
(2)思考:如图1,当线段CD所在直线与半圆O相切时,求弧BD的长. 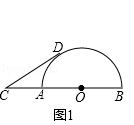
(3)探究:如图2,当线段CD与半圆O有两个公共点D,M时,若CM=DM,求等边△CDE面积. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知凸四边形ABCD中,∠A=∠C=90°.
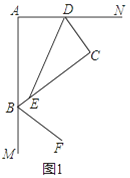
(1)如图1,若DE平分∠ADC,BF平分∠ABC的邻补角,判断DE与BF位置关系并证明.
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
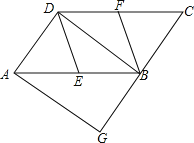
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
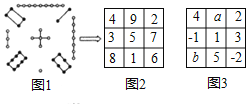
【题目】(阅读材料)“九宫图”源于我国古代夏禹时期的“洛书”![]() 图1所示
图1所示![]() ,是世界上最早的矩阵,又称“幻方”,用今天的数学符号翻译出来,“洛书”就是一个三阶“幻方”
,是世界上最早的矩阵,又称“幻方”,用今天的数学符号翻译出来,“洛书”就是一个三阶“幻方”![]() 图2所示
图2所示![]() .
.
(规律总结)观察图1、图2,根据“九宫图”中各数字之间的关系,我们可以总结出“幻方”需要满足的条件是______;若图3,是一个“幻方”,则![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式![]() ,当
,当![]() 时,该代数式的值为-1.
时,该代数式的值为-1.
(1)求![]() 的值。
的值。
(2)已知当![]() 时,该代数式的值为-1,求
时,该代数式的值为-1,求![]() 的值。
的值。
(3)已知当![]() 时,该代数式的值为9,试求当
时,该代数式的值为9,试求当![]() 时该代数式的值。
时该代数式的值。
(4)在第(3)小题已知条件下,若有![]() 成立,试比较
成立,试比较![]() 与
与![]() 的大小。
的大小。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反映的是某中学九(3)班学生外出方式(乘车、步行、骑车)的频数(人数)分布直方图(部分)和扇形分布图,那么下列说法正确的是( )
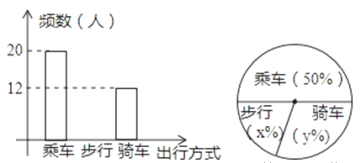
A. 九(3)班外出的学生共有42人
B. 九(3)班外出步行的学生有8人
C. 在扇形图中,步行的学生人数所占的圆心角为82°
D. 如果该校九年级外出的学生共有500人,那么估计全年级外出骑车的学生约有140人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com