
【题目】已知凸四边形ABCD中,∠A=∠C=90°.
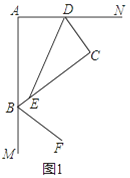
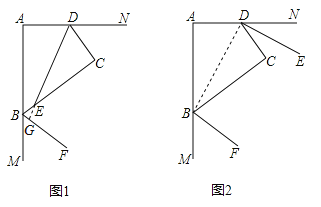
(1)如图1,若DE平分∠ADC,BF平分∠ABC的邻补角,判断DE与BF位置关系并证明.
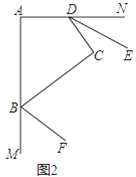
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.
【答案】见解析
【解析】试题分析:(1)DE⊥BF,延长DE交BF于G.易证∠ADC=∠CBM.可得∠CDE=∠EBF.即可得∠EGB=∠C=90゜,则可证得DE⊥BF;
(2)DE∥BF,连接BD,易证∠NDC+∠MBC=180゜,则可得∠EDC+∠CBF=90゜,继而可证得∠EDC+∠CDB+∠CBD+∠FBC=180゜,则可得DE∥BF.
试题解析:解:(1)DE⊥BF.证明如下:
延长DE交BF于点G.∵∠A+∠ABC+∠C+∠ADC=360°,∠A=∠C=90°,∴∠ABC+∠ADC=180°.∵∠ABC+∠MBC=180°,∴∠ADC=∠MBC.∵DE、BF分别平分∠ADC、∠MBC,∴∠EDC=![]() ∠ADC,∠EBG=
∠ADC,∠EBG=![]() ∠MBC,∴∠EDC=∠EBG.∵∠EDC+∠DEC+∠C=180°,∠EBG+∠BEG+∠EGB=180°,∠DEC=∠BEG,∴∠EGB=∠C=90°,∴DE⊥BF;
∠MBC,∴∠EDC=∠EBG.∵∠EDC+∠DEC+∠C=180°,∠EBG+∠BEG+∠EGB=180°,∠DEC=∠BEG,∴∠EGB=∠C=90°,∴DE⊥BF;
(2)DE∥BF.证明如下:
连接BD.∵DE、BF分别平分∠NDC、∠MBC,∴∠EDC=![]() ∠NDC,∠FBC=
∠NDC,∠FBC=![]() ∠MBC.
∠MBC.
∵∠ADC+∠NDC=180°,∠ADC=∠MBC,∴∠MBC+∠NDC=180°,∴∠EDC+∠FBC=90°.
∵∠C=90°,∴∠CDB+∠CBD=90°,∴∠EDC+∠CDB+∠FBC+∠CBD=180°,即∠EDB+∠FBD=180°,∴DE∥BF.


科目:初中数学 来源: 题型:
【题目】如图,两同心圆的圆心为O,大圆的弦AB与小圆相切于点P,已知两圆的半径分别为2和1,用阴影部分围成一个圆锥(OA与OB重合),则该圆锥的底面半径是( ) 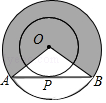
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台在它的娱乐性节目中每期抽出两名场外幸运观众,有一期甲、乙两人被抽为场外幸运观众,他们获得了一次抽奖的机会,在如图所示的翻奖牌的正面4个数字中任选一个,选中后翻开,可以得到该数字反面的奖品,第一个人选中的数字第二个人不能再选择了. 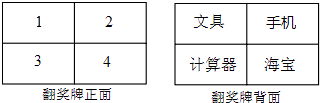
(1)如果甲先抽奖,那么甲获得“手机”的概率是多少?
(2)小亮同学说:甲先抽奖,乙后抽奖,甲、乙两人获得“手机”的概率不同,且甲获得“手机”的概率更大些.你同意小亮同学的说法吗?为什么?请用列表或画树状图分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧 ![]() 、
、 ![]() 是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )
是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )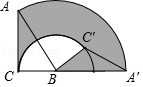
A.4π+2 ![]()
B.![]()
π﹣2 ![]()
C.![]()
π+2 ![]()
D.4π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△AOB中,将扇形COD按图1摆放,使扇形的半径OC、OD分别与OA、OB重合,OA=OB=2,OC=OD=1,固定等边△AOB不动,让扇形COD绕点O逆时针旋转,线段AC、BD也随之变化,设旋转角为α.(0<α≤360°) 
(1)当OC∥AB时,旋转角α=度;
(2)线段AC与BD有何数量关系,请仅就图2给出证明. 
(3)当A、C、D三点共线时,求BD的长.
(4)P是线段AB上任意一点,在扇形COD的旋转过程中,请直接写出线段PC的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正方体的六个面分别涂上六种不同颜色,并画上朵数不等的花,各面上的颜色与花的朵数情况见下表:
现将上述大小相同,颜色、花朵分布也完全相同的四个正方体拼成一个水平放置的长方体,如图所示.问长方体的下底面共有多少朵花?
颜色 | 红 | 黄 | 蓝 | 白 | 紫 | 绿 |
花的朵数 | 1 | 2 | 3 | 4 | 5 | 6 |
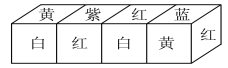
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时.求证:CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;
①请直接写出CF,BC,CD三条线段之间的关系;
②若正方形ADEF的边长为2![]() ,对角线AE,DF相交于点O,连接OC.求OC的长度.
,对角线AE,DF相交于点O,连接OC.求OC的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com