
【题目】已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时.求证:CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;
①请直接写出CF,BC,CD三条线段之间的关系;
②若正方形ADEF的边长为2![]() ,对角线AE,DF相交于点O,连接OC.求OC的长度.
,对角线AE,DF相交于点O,连接OC.求OC的长度.

【答案】(1)证明见解析;(2)CF-CD=BC;(3)①CD-CF=BC;②2.
【解析】试题分析:(1)、根据正方形的性质判定出△BAD和△CAF全等,从而得出BD=CF,根据BD+CD=BC得出答案;(2)、根据图形得出线段之间的关系;(3)、首先根据正方形的性质证明△BAD和△CAF全等,然后得出∠ACF=∠ABD=135°,从而说明△FCD为直角三角形,根据正方形的对角线得出DF的长度,然后根据直角三角形斜边上的中线的性质得出OC的长度.
试题解析:(1)、∵∠BAC=90°,∠ABC=45°,∴∠ACB=∠ABC=45°,∴AB=AC,
∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°,
∵∠BAD=90°-∠DAC,∠CAF=90°-∠DAC,∴∠BAD=∠CAF,
则在△BAD和△CAF中,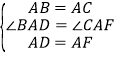 ∴△BAD ≌ △CAF(SAS),∴BD=CF,
∴△BAD ≌ △CAF(SAS),∴BD=CF,
∵BD+CD=BC,∴CF+CD=BC;
(2)、CF-CD=BC
(3)、①CD-CF =BC.
②∵∠BAC=90°,∠ABC=45°,∴∠ACB=∠ABC=45°,∴AB=AC, ∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°, ∵∠BAD=90°-∠BAF,∠CAF=90°-∠BAF,∴∠BAD=∠CAF,
则在△BAD和△CAF中,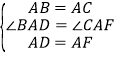 ∴△BAD ≌ △CAF(SAS),
∴△BAD ≌ △CAF(SAS),
∴∠ABD=∠ACF,∵∠ABC=45°,∠ABD=135°, ∴∠ACF=∠ABD=135°,
∴∠FCD=90°,∴△FCD是直角三角形. ∵正方形ADEF的边长为![]() 且对角线AE、DF相交于点O,
且对角线AE、DF相交于点O,
∴DF=![]() AD=4,O为DF中点. ∴OC=
AD=4,O为DF中点. ∴OC=![]() DF=2.
DF=2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为迎接2008年北京奥运会,某学校组织了一次野外长跑活动,参加长跑的同学出发后,另一些同学从同地骑自行车前去加油助威。如图,线段L1,L2分别表示长跑的同学和骑自行车的同学行进的路程y(千米)随时间x(分钟)变化的函数图象.根据图象,解答下列问题:
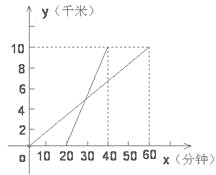
(1)分别求出长跑的同学和骑自行车的同学的行进路程y与时间x的函数表达式;
(2)求长跑的同学出发多少时间后,骑自行车的同学就追上了长跑的同学?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,直线l3和直线l1,l2交于点C和D,直线l3上有一点P.
(1)如图1,若P点在C,D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化,并说明理由;
(2)若点P在C,D两点的外侧运动时(P点与点C,D不重合,如图2和3),试直接写出∠PAC,∠APB,∠PBD之间的关系,不必写理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店去年8月底购进了一批文具1160件,预计在9月份进行试销.购进价格为每件10元.若售价为12元/件,则可全部售出.若每涨价0.1元.销售量就减少2件.
(1)求该文具店在9月份销售量不低于1100件,则售价应不高于多少元?
(2)由于销量好,10月份该文具进价比8月底的进价每件增加20%,该店主增加了进货量,并加强了宣传力度,结果10月份的销售量比9月份在(1)的条件下的最低销售量增加了m%,但售价比9月份在(1)的条件下的最高售价减少![]() m%.结果10月份利润达到3388元,求m的值(m>10).
m%.结果10月份利润达到3388元,求m的值(m>10).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.小美根据学习函数的经验,对函数
的图象与性质.小美根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
(![]() )函数
)函数![]() 的自变量
的自变量![]() 的取值范围是__________.
的取值范围是__________.
(![]() )下表是
)下表是![]() 与
与![]() 的几组对应值.
的几组对应值.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
如图,在平面直角坐标系![]() 中,描出以上表中各对对应值为坐标的点.
中,描出以上表中各对对应值为坐标的点.
根据描出的点,画出该函数的图象,标出函数的解析式.

(![]() )结合函数的图象,写出该函数的一条性质:__________.
)结合函数的图象,写出该函数的一条性质:__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )

A. 8 B. 16 C. 24 D. 32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,下列结论中不正确的是( )

A. ∠BAC=70° B. ∠DOC=90° C. ∠BDC=35° D. ∠DAC=55°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com