
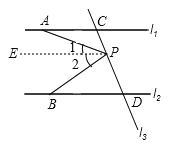
【题目】如图,已知直线l1∥l2,直线l3和直线l1,l2交于点C和D,直线l3上有一点P.
(1)如图1,若P点在C,D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化,并说明理由;
(2)若点P在C,D两点的外侧运动时(P点与点C,D不重合,如图2和3),试直接写出∠PAC,∠APB,∠PBD之间的关系,不必写理由.

【答案】(1)当P点在C,D之间运动时,∠APB=∠PAC+∠PBD (2)当点P在C,D两点的外侧运动时,在l2下方时,则∠PAC=∠PBD+∠APB;在l1上方时,则∠PBD=∠PAC+∠APB.
【解析】试题分析:(1)当P点在C、D之间运动时,首先过点P作PE∥l1,由l1∥l2,可得PE∥l2∥l1,根据两直线平行,内错角相等,即可求得:∠APB=∠PAC+∠PBD.
(2)当点P在C、D两点的外侧运动时,由直线l1∥l2,根据两直线平行,同位角相等与三角形外角的性质,即可求得:∠PAC=∠PBD+∠APB或∠PBD=∠PAC+∠APB.
试题解析:解:(1)如图①,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD.
理由如下:
过点P作PE∥l1,∵l1∥l2,∴PE∥l2∥l1,∴∠PAC=∠1,∠PBD=∠2,∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)如图2,当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.
理由如下:
∵l1∥l2,∴∠PED=∠PAC,∵∠PED=∠PBD+∠APB,∴∠PAC=∠PBD+∠APB.
如图3,当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由如下:
∵l1∥l2,∴∠PEC=∠PBD,∵∠PEC=∠PAC+∠APB,∴∠PBD=∠PAC+∠APB.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】新学期开学,某体育用品商店开展促销活动,有两种优惠方案.
方案一:不购买会员卡时,乒乓球享受8.5折优惠,乒乓球拍购买5副(含5副)以上才能享受8.5折优惠,5副以下必须按标价购买.
方案二:办理会员卡时,全部商品享受八折优惠,小健和小康的谈话内容如下:

会员卡只限本人使用.
(1)求该商店销售的乒乓球拍每副的标价.
(2)如果乒乓球每盒10元,小健需购买乒乓球拍6副,乒乓球a盒,请回答下列问题:
①如果方案一与方案二所付钱数一样多,求a的值;
②直接写出一个恰当的a值,使方案一比方案二优惠;
③直接写出一个恰当的a值,使方案二比方案一优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,AC=8m,BC=6m,点P由C点出发以2m/s的速度向终点A匀速移动,同时点Q由点B出发以1m/s的速度向终点C匀速移动,当一个点到达终点时另一个点也随之停止移动.
(1)经过几秒△PCQ的面积为△ACB的面积的![]() ?
?
(2)经过几秒,△PCQ与△ACB相似?
(3)如图2,设CD为△ACB的中线,那么在运动的过程中,PQ与CD有可能互相垂直吗?若有可能,求出运动的时间;若没有可能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 (1),已知△ABC是等边三角形,以BC为直径的⊙O交AB、AC于D、E.求证:

(1)△DOE是等边三角形.
(2)如图(2),若∠A=60°,AB≠AC, 则(1)中结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
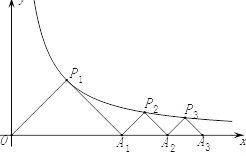
【题目】如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)在函数y=![]() (x>0)的图象上,△P1OA1, △P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),
(x>0)的图象上,△P1OA1, △P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),
(1)求点P1, P2, P3的坐标.
(2)猜想并直接写出点Pn的坐标(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种饮料,平均每天可售出100箱,每箱利润120元.天气渐热,为了扩大销售,增加利润,超市准备适当降价.据测算,若每箱饮料每降价1元,每天可多售出2箱.针对这种饮料的销售情况,请解答以下问题:
(1)当每箱饮料降价20元时,这种饮料每天销售获利多少元?
(2)在要求每箱饮料获利大于80元的情况下,要使每天销售饮料获利14400元,问每箱应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时.求证:CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;
①请直接写出CF,BC,CD三条线段之间的关系;
②若正方形ADEF的边长为2![]() ,对角线AE,DF相交于点O,连接OC.求OC的长度.
,对角线AE,DF相交于点O,连接OC.求OC的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绿豆在相同条件下的发芽试验,结果如下表所示:
每批 粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的 粒数m | 96 | 282 | 382 | 570 | 948 | 1912 | 2850 |
发芽的 频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.956 | 0.950 |
则绿豆发芽的概率估计值是( )
A. 0.96 B. 0.95 C. 0.94 D. 0.90
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京沈高铁赤峰至喀左段于2016年开工建设,天义镇路基桥墩建设初具规模,预计2019年运营,从赤峰出发经宁城至北京500公里,高铁运行速度将是现行普通客车平均速度的5倍,预计开通后,从赤峰出发,某高铁客运专列比普通客车晚3小时开出,但比普通客车早5小时到达北京,求两车的运行速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com