
【题目】如图 (1),已知△ABC是等边三角形,以BC为直径的⊙O交AB、AC于D、E.求证:

(1)△DOE是等边三角形.
(2)如图(2),若∠A=60°,AB≠AC, 则(1)中结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
【答案】(1)证明见解析(2)当∠A=60°,AB≠AC时,(1)中的结论仍然成立
【解析】试题分析:(1)、根据等边三角形的性质以及圆的半径可以得出:△OBD和△OEC都为等边三角形,结合∠BOD=∠EOC=60°得出∠DOE=60°,从而得出等边三角形;(2)、连接CD,根据BC为直径得出∠BDC=∠ADC=90°,根据∠A的度数得出∠ACD=30°,然后根据圆周角的性质可得:∠DOE=60°,结合OD=OE得出等边三角形.
试题解析:(1)、证明:∵△ABC为等边三角形, ∴∠B=∠C=60°,
∵OB=OC=OE=OD ,∴△OBD和△OEC都为等边三角形,
∴∠BOD=∠EOC=60°, ∴∠DOE=60°, ∴△DOE为等边三角形.
(2)、解:当∠A=60°,AB≠AC时,(1)中的结论仍然成立.
证明:连结CD,∵BC为⊙O的直径, ∴∠BDC=90°, ∴∠ADC=90°, ∵∠A=60°,
∴∠ACD=30°, ∴∠DOE=2∠ACD=60°, ∵OD=OE ,∴△DOE为等边三角形.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
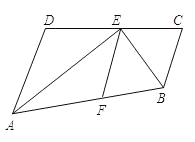
【题目】如图,点E在线段CD上,EA、EB分别平分∠DAB和∠CBA,点F在线段AB上运动,AD=4cm,BC=3cm,且AD∥BC.
(1)你认为AE和BE有什么位置关系?并验证你的结论;
(2)当点F运动到离点A多少厘米时,△ADE和△AFE全等?为什么?
(3)在(2)的情况下,此时BF=BC吗?证明你的结论并求出AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M,N分别是AC,BC的中点,求线段MN的长度.
![]()
(2)在(1)中,如果AC=acm,BC=bcm,其它条件不变,你能猜出MN的长度吗?请你用一句简洁的话表述你发现的规律.
(3)对于(1)题,如果我们这样叙述它:“已知线段AC=6cm,BC=4cm,点C在直线AB上,点M,N分别是AC,BC的中点,求MN的长度.”结果会有变化吗?如果有,求出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠C=90°,点D,E分别是△ABC边AC,BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图①所示,且∠α=50°,则∠1+∠2=________°;
(2)若点P在边AB上运动,如图②所示,则∠α,∠1,∠2之间的关系为:____________;

(3)若点P运动到边AB的延长线上,如图③所示,则∠α,∠1,∠2之间有何关系?猜想并说明理由;

(4)若点P运动到△ABC形外,如图④所示,则∠α,∠1,∠2之间的关系为:____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的![]() .
.
(1)求配色条纹的宽度;
(2)如果地毯配色条纹部分每平方米造价200元,其余部分每平方米造价100元,求地毯的总造价.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,直线l3和直线l1,l2交于点C和D,直线l3上有一点P.
(1)如图1,若P点在C,D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化,并说明理由;
(2)若点P在C,D两点的外侧运动时(P点与点C,D不重合,如图2和3),试直接写出∠PAC,∠APB,∠PBD之间的关系,不必写理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.小美根据学习函数的经验,对函数
的图象与性质.小美根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
(![]() )函数
)函数![]() 的自变量
的自变量![]() 的取值范围是__________.
的取值范围是__________.
(![]() )下表是
)下表是![]() 与
与![]() 的几组对应值.
的几组对应值.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
如图,在平面直角坐标系![]() 中,描出以上表中各对对应值为坐标的点.
中,描出以上表中各对对应值为坐标的点.
根据描出的点,画出该函数的图象,标出函数的解析式.

(![]() )结合函数的图象,写出该函数的一条性质:__________.
)结合函数的图象,写出该函数的一条性质:__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正、减产记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | +5 | ﹣2 | ﹣4 | +12 | ﹣10 | +16 | ﹣9 |
(1)根据记录的数据可知该厂星期六生产自行车______辆;
(2)根据记录的数据可知该厂本周实际生产自行车_____辆;
(3)产量最多的一天比产量最少的一天多生产自行车_____辆;
(4)该厂实行每周计件工资制,每生产一辆车可得50元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣20元,那么该厂工人这一周的工资总额是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com