
【题目】某超市销售一种饮料,平均每天可售出100箱,每箱利润120元.天气渐热,为了扩大销售,增加利润,超市准备适当降价.据测算,若每箱饮料每降价1元,每天可多售出2箱.针对这种饮料的销售情况,请解答以下问题:
(1)当每箱饮料降价20元时,这种饮料每天销售获利多少元?
(2)在要求每箱饮料获利大于80元的情况下,要使每天销售饮料获利14400元,问每箱应降价多少元?
【答案】(1)14000元;(2)30元
【解析】试题分析:
(1)由题意可知,每箱降价20元时,每箱利润为:(120-20)元,销售量为(100+20×2)箱,两者相乘可得每天获利总额;
(2)这每箱应降价![]() 元,则此时每箱获利为(120-
元,则此时每箱获利为(120- ![]() )元,销售量为(100+
)元,销售量为(100+![]() )箱,由二者相乘等于总利润14400可列方程,解方程求得
)箱,由二者相乘等于总利润14400可列方程,解方程求得![]() ,再结合“每箱获利大于80元”进行检验可得结果.
,再结合“每箱获利大于80元”进行检验可得结果.
试题解析:
(1)当每箱降价20元时,由题意可得此时每天可获利润为:
(120-20)×(100+2×20)=14000(元).
(2)要使每天销售饮料获利14400元,每箱应降价![]() 元,依据题意列方程得:
元,依据题意列方程得:
![]()
整理得: ![]() ,
,
解得: ![]() ,
,
∵ 要求每箱饮料获利大于80元,
∴ ![]() .
.
答:每箱应降价30元,可使每天销售饮料获利14400元.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AD∥CB,∠A=∠C,若∠ABD=32°,求∠BDC的度数.有同学用了下面的方法.但由于一时犯急没有写完整,请你帮他添写完整.
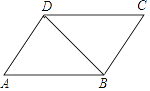
解:∵AD∥CB(已知)
∴∠C+∠ADC=180°(_________________),
又∵∠A=∠C (___________________),
∴∠A+∠ADC=180° (___________________),
∴AB∥CD (___________________________),
∴∠BDC=∠ABD=32° (___________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠C=90°,点D,E分别是△ABC边AC,BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图①所示,且∠α=50°,则∠1+∠2=________°;
(2)若点P在边AB上运动,如图②所示,则∠α,∠1,∠2之间的关系为:____________;

(3)若点P运动到边AB的延长线上,如图③所示,则∠α,∠1,∠2之间有何关系?猜想并说明理由;

(4)若点P运动到△ABC形外,如图④所示,则∠α,∠1,∠2之间的关系为:____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的![]() .
.
(1)求配色条纹的宽度;
(2)如果地毯配色条纹部分每平方米造价200元,其余部分每平方米造价100元,求地毯的总造价.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,直线l3和直线l1,l2交于点C和D,直线l3上有一点P.
(1)如图1,若P点在C,D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化,并说明理由;
(2)若点P在C,D两点的外侧运动时(P点与点C,D不重合,如图2和3),试直接写出∠PAC,∠APB,∠PBD之间的关系,不必写理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)9(y+4)2﹣49=0
(2)2x2+3=7x(配方法);
(3)2x2﹣7x+5=0 (公式法)
(4)x2=6x+16
(5)2x2﹣7x﹣18=0
(6)(2x﹣1)(x+3)=4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.小美根据学习函数的经验,对函数
的图象与性质.小美根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
(![]() )函数
)函数![]() 的自变量
的自变量![]() 的取值范围是__________.
的取值范围是__________.
(![]() )下表是
)下表是![]() 与
与![]() 的几组对应值.
的几组对应值.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
如图,在平面直角坐标系![]() 中,描出以上表中各对对应值为坐标的点.
中,描出以上表中各对对应值为坐标的点.
根据描出的点,画出该函数的图象,标出函数的解析式.

(![]() )结合函数的图象,写出该函数的一条性质:__________.
)结合函数的图象,写出该函数的一条性质:__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条直线上依次有![]() 、
、![]() 、
、![]() 三个港口,甲、乙两船同时分别从
三个港口,甲、乙两船同时分别从![]() 、
、![]() 港口出发,沿直线匀速驶向
港口出发,沿直线匀速驶向![]() 港,最终达到
港,最终达到![]() 港.设甲、乙两船行驶
港.设甲、乙两船行驶![]() 后,与
后,与![]() 港的距离分别为
港的距离分别为![]() 、
、![]() ,
,![]() 、
、![]() 与
与![]() 的函数关系如图所示.
的函数关系如图所示.
(![]() )填空:
)填空:![]() 、
、![]() 两港口间的距离为__________
两港口间的距离为__________![]() ,
,![]() __________.
__________.
(![]() )求图中点
)求图中点![]() 的坐标.
的坐标.
(![]() )若两船的距离不超过
)若两船的距离不超过![]() 时能够相互望见,求甲、乙两船可以相互望见时
时能够相互望见,求甲、乙两船可以相互望见时![]() 的取值范围.
的取值范围.
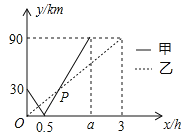
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=x+1,反比例函数y=![]() .
.
(1)当k为何值时,这两个函数的图象有两个交点?
(2)当k为何值时,这两个函数的图象没有交点?
(3)这两个函数的图象能否只有一个交点?若有,求出这个交点坐标;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com