
【题目】解下列方程:
(1)9(y+4)2﹣49=0
(2)2x2+3=7x(配方法);
(3)2x2﹣7x+5=0 (公式法)
(4)x2=6x+16
(5)2x2﹣7x﹣18=0
(6)(2x﹣1)(x+3)=4.
【答案】(1)y1=﹣![]() ,y2=﹣
,y2=﹣![]() ;(2)x1=3,x2=
;(2)x1=3,x2=![]() ;(3)x1=2.5,x2=1;(4)x1=﹣2,x2=8(5)x=
;(3)x1=2.5,x2=1;(4)x1=﹣2,x2=8(5)x=![]() ;(6)x1=﹣3.5,x2=1.
;(6)x1=﹣3.5,x2=1.
【解析】试题分析:
(1)用“直接开平方法”解此方程即可;
(2)、(3)按指定方法解方程即可;
(4)先将方程化为一般形式,再用“因式分解法”解此方程:
(5)用“公式法”解此方程即可;
(6)先整理为一般形式,再用“因式分解法”解此方程.
试题解析:
(1)方程可化为:(y+4)2=![]() ,
,
开方得:y+4=±![]() ,
,
解得:y1=﹣![]() ,y2=﹣
,y2=﹣![]() ;
;
(2)方程整理得:x2﹣![]() x=﹣
x=﹣![]() ,
,
配方得:x2﹣![]() x+
x+![]() =
=![]() ,即(x﹣
,即(x﹣![]() )2=
)2=![]() ,
,
开方得:x﹣![]() =±
=±![]() ,
,
解得:x1=3,x2=![]() ;
;
(3)∵在方程2x2﹣7x+5=0中,a=2,b=﹣7,c=5,
∴△=49﹣40=9,
∴x=![]() ,
,
解得:x1=2.5,x2=1;
(4)原方程整理得:x2﹣6x﹣16=0,即(x+2)(x﹣8)=0,
解得:x1=﹣2,x2=8;
(5)∵在方程2x2﹣7x﹣18=0
中,a=2,b=﹣7,c=﹣18,
∵△=49+144=193,
∴ x=![]() ;
;
∴![]() ,
, ![]() .
.
(6)原方程整理得:2x2+5x﹣7=0,
即(2x+7)(x﹣1)=0,
解得:x1=﹣3.5,x2=1.


科目:初中数学 来源: 题型:
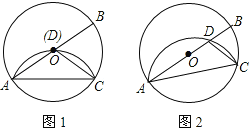
【题目】⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.
(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r;
(2)如图2,若点D与圆心O不重合,∠BAC=25°,求∠DCA的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
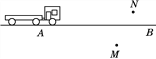
【题目】如图,M,N为坐落于公路两旁的村庄,如果一辆施工的机动车由A向B行驶,产生的噪音会对两个村庄造成影响.
(1)当施工车行驶到何处时,产生的噪音分别对两个村庄影响最大?在图中标出来.
(2)当施工车从A向B行驶时,产生的噪音对M,N两个村庄的影响情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
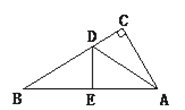
【题目】如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿∠CAB的角平分线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种饮料,平均每天可售出100箱,每箱利润120元.天气渐热,为了扩大销售,增加利润,超市准备适当降价.据测算,若每箱饮料每降价1元,每天可多售出2箱.针对这种饮料的销售情况,请解答以下问题:
(1)当每箱饮料降价20元时,这种饮料每天销售获利多少元?
(2)在要求每箱饮料获利大于80元的情况下,要使每天销售饮料获利14400元,问每箱应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=21,EC=9,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C为一个平行四边形的三个顶点,且A,B,C三点的坐标分别为(3,3),(6,4),(4,6).
(1)请直接写出这个平行四边形第四个顶点的坐标;
(2)求这个平行四边形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】安宁市的一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元,若经粗加工后销售,每吨利润可达4500元;若经精加工后销售每吨获利7500元.当地一家农产品企业收购这种蔬菜140吨,该企业加工厂的生产能力是:如果对蔬菜进行粗加工,每天可以加工16吨,如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节条件限制,企业必须在15天的时间将这批蔬菜全部销售或加工完毕,企业研制了四种可行方案:
方案一:全部直接销售;
方案二:全部进行粗加工;
方案三:尽可能多地进行精加工,没有来得及进行精加工的直接销售;
方案四:将一部分进行精加工,其余的进行粗加工,并恰好15天完成.
请通过计算以上四个方案的利润,帮助企业选择一个最佳方案使所获利润最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,记录球的颜色,放回盒中,然后重复上述过程。
活动结果:摸球实验活动一共做了50次,统计结果如下表:

推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com