
【题目】已知函数y=x+1,反比例函数y=![]() .
.
(1)当k为何值时,这两个函数的图象有两个交点?
(2)当k为何值时,这两个函数的图象没有交点?
(3)这两个函数的图象能否只有一个交点?若有,求出这个交点坐标;若没有,请说明理由.
【答案】(1)k>-![]() 且k≠ 0;(2)k<-
且k≠ 0;(2)k<-![]() ;(3)k=-
;(3)k=-![]() ,交点坐标为(-
,交点坐标为(-![]() ,
, ![]() )
)
【解析】试题分析:这两个函数的图象有两个交点,即联立后方程组有两个解;两个函数的图象没有交点,即联立后方程组无解;两个函数的图象有一个交点,即联立后方程组有两个相等的解据此联立两个函数的解析式,根据对称性解出答案即可;
试题解析:解:联立解析式: 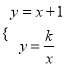 ,可得:x+1=
,可得:x+1=![]() ,∵x≠0,∴x2+x﹣k=0,(1)若两个函数的图象有两个交点,则△=1+4k>0,解得:k>﹣
,∵x≠0,∴x2+x﹣k=0,(1)若两个函数的图象有两个交点,则△=1+4k>0,解得:k>﹣![]() 且k≠0;
且k≠0;
(2)若两个函数的图象没有交点,则△=1+4k<0,解得:k>﹣![]() .
.
(3)两个函数的图象只有一个交点,则△=1+4k=0,解得:k=﹣![]() ,∴x2+x+
,∴x2+x+![]() =0.解得,x=﹣
=0.解得,x=﹣![]() ,代入y=x+1得,y=
,代入y=x+1得,y=![]() ,∴这个交点坐标为(﹣
,∴这个交点坐标为(﹣![]() ,
, ![]() ).
).


科目:初中数学 来源: 题型:
【题目】某超市销售一种饮料,平均每天可售出100箱,每箱利润120元.天气渐热,为了扩大销售,增加利润,超市准备适当降价.据测算,若每箱饮料每降价1元,每天可多售出2箱.针对这种饮料的销售情况,请解答以下问题:
(1)当每箱饮料降价20元时,这种饮料每天销售获利多少元?
(2)在要求每箱饮料获利大于80元的情况下,要使每天销售饮料获利14400元,问每箱应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
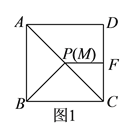
【题目】正方形![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,
的中点,![]() 是对角线
是对角线![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 于点
于点![]() .如图
.如图![]() ,当点
,当点![]() 与点
与点![]() 重合时,显然有
重合时,显然有![]() .
.
(![]() )如图
)如图![]() ,若点
,若点![]() 在线段
在线段![]() 上(不与点
上(不与点![]() 、
、![]() 重合),
重合),![]() 且
且![]() 交
交![]() 于点
于点![]() .
.
求证:![]() .
.
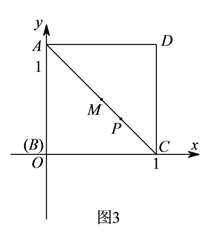
(![]() )如图所示建立直角坐标系,且正方形
)如图所示建立直角坐标系,且正方形![]() 的边长为
的边长为![]() ,若点
,若点![]() 在线段
在线段![]() 上(不与点
上(不与点![]() 、
、![]() 重合),
重合),![]() ,且
,且![]() 交直线
交直线![]() 于点
于点![]() .请在图
.请在图![]() 中作出示意图,并且求出当
中作出示意图,并且求出当![]() 是一个等腰三角形时,
是一个等腰三角形时,![]() 点的坐标为__________(直接写出答案).
点的坐标为__________(直接写出答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,动点P在函数y=![]() (x>0)的图象上运动,PM⊥x轴于M,PN⊥y轴于N,线段PM、PN分别与直线AB:y=-x+1交于点E、F,且AFBE的值为1,则k为________.
(x>0)的图象上运动,PM⊥x轴于M,PN⊥y轴于N,线段PM、PN分别与直线AB:y=-x+1交于点E、F,且AFBE的值为1,则k为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京沈高铁赤峰至喀左段于2016年开工建设,天义镇路基桥墩建设初具规模,预计2019年运营,从赤峰出发经宁城至北京500公里,高铁运行速度将是现行普通客车平均速度的5倍,预计开通后,从赤峰出发,某高铁客运专列比普通客车晚3小时开出,但比普通客车早5小时到达北京,求两车的运行速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,记录球的颜色,放回盒中,然后重复上述过程。
活动结果:摸球实验活动一共做了50次,统计结果如下表:

推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() (k1>0)与一次函数y=k2x+1(k2≠0)的图象交于A,B
(k1>0)与一次函数y=k2x+1(k2≠0)的图象交于A,B
两点,AC⊥x轴于点C.若△OAC的面积为1,且AC=2OC.
(1)求反比例函数与一次函数的解析式;
(2)请直接写出点B的坐标;
(3)当x为何值时,反比例函数的值大于一次函数的值?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=10cm,BC=8cm,点E是CD的中点,动点P从A点出发,以每秒2cm的速度沿A→B→C→E运动,最终到达点E.若点P运动的时间为x秒,那么当x= 时,△APE的面积等于32.

查看答案和解析>>
科目:初中数学 来源: 题型:
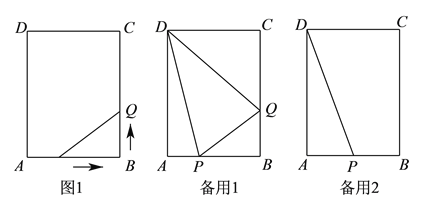
【题目】如图![]() ,在长方形
,在长方形![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 从点
从点![]() 开始以
开始以![]() 的速度沿
的速度沿![]() 边向点
边向点![]() 运动,点
运动,点![]() 从点
从点![]() 以
以![]() 的速度沿
的速度沿![]() 边向点
边向点![]() 运动,如果
运动,如果![]() 、
、![]() 同时出发,设运动时间为
同时出发,设运动时间为![]() .
.
(![]() )当
)当![]() 时,求
时,求![]() 的长.
的长.
(![]() )当点
)当点![]() 运动到点
运动到点![]() 时,
时, ![]() 、
、![]() 同时停止运动.在运动过程中,是否存在
同时停止运动.在运动过程中,是否存在![]() 的值,使得
的值,使得![]() 、
、![]() 、
、![]() 的面积都相等,若存在,求出
的面积都相等,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(![]() )当运动
)当运动![]() 时,
时, ![]() 点停止运动,
点停止运动, ![]() 点以原速立即向
点以原速立即向![]() 点返回,在返回的过程中,
点返回,在返回的过程中, ![]() 是否能平分
是否能平分![]() ?若能,求出点
?若能,求出点![]() 运动的时间;若不能,请说明理由.
运动的时间;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com