
【题目】如图,在正方形网格中,点A、B、C、M、N都在格点上(不写作法)
(1)作△ABC关于直线MN对称的△A’B’C’:
(2)将△ABC向上平移两个单位得△A1B1C1,画出△A1B1C1;
(3)在直线MN上找一点P,使AP+CP的值最小.
(4)若网格中最小正方形的边长为1,直接写出△ABC的面积.

科目:初中数学 来源: 题型:
【题目】若关于x的不等式x﹣ ![]() <1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
<1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
A.有两个相等的实数根
B.有两个不相等的实数根
C.无实数根
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两同心圆的圆心为O,大圆的弦AB与小圆相切于点P,已知两圆的半径分别为2和1,用阴影部分围成一个圆锥(OA与OB重合),则该圆锥的底面半径是( ) 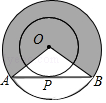
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:
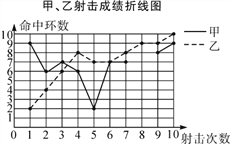
甲、乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中10环的次数 | |
甲 | 7 | |||
乙 | 1 |
(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁将胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备举行社团活动,需要向商家购买A,B两种型号的文化衫50件,己知一件A型号文化衫的售价比一件B型号文化衫的售价贵9元,用200元恰好可以买到2件A型号文化衫和S件B型号文化杉.
(1)求A、B两种型号的文化衫每件的价格分别为多少元?
(2)如果用于购买A、B两种型号文化杉的金额不少于1500元但不超过1530元,请体求出所有的购买方案?
(3)试问在(2)的条件下,学校采用哪种购买方案花钱最少?最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料: 如图1,圆的概念:在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上,圆心在P(a,b),半径为r的圆的方程可以写为:(x﹣a)2+(y﹣b)2=r2 , 如:圆心在P(2,﹣1),半径为5的圆方程为:(x﹣2)2+(y+1)2=25
(1)填空: ①以A(3,0)为圆心,1为半径的圆的方程为;
②以B(﹣1,﹣2)为圆心, ![]() 为半径的圆的方程为 .
为半径的圆的方程为 .
(2)根据以上材料解决下列问题: 如图2,以B(﹣6,0)为圆心的圆与y轴相切于原点,C是⊙B上一点,连接OC,作BD⊥OC垂足为D,延长BD交y轴于点E,已知sin∠AOC= ![]() .
.
①连接EC,证明EC是⊙B的切线;
②在BE上是否存在一点P,使PB=PC=PE=PO?若存在,求P点坐标,并写出以P为圆心,以PB为半径的⊙P的方程;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台在它的娱乐性节目中每期抽出两名场外幸运观众,有一期甲、乙两人被抽为场外幸运观众,他们获得了一次抽奖的机会,在如图所示的翻奖牌的正面4个数字中任选一个,选中后翻开,可以得到该数字反面的奖品,第一个人选中的数字第二个人不能再选择了. 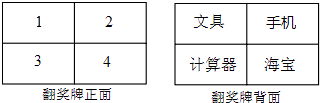
(1)如果甲先抽奖,那么甲获得“手机”的概率是多少?
(2)小亮同学说:甲先抽奖,乙后抽奖,甲、乙两人获得“手机”的概率不同,且甲获得“手机”的概率更大些.你同意小亮同学的说法吗?为什么?请用列表或画树状图分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△AOB中,将扇形COD按图1摆放,使扇形的半径OC、OD分别与OA、OB重合,OA=OB=2,OC=OD=1,固定等边△AOB不动,让扇形COD绕点O逆时针旋转,线段AC、BD也随之变化,设旋转角为α.(0<α≤360°) 
(1)当OC∥AB时,旋转角α=度;
(2)线段AC与BD有何数量关系,请仅就图2给出证明. 
(3)当A、C、D三点共线时,求BD的长.
(4)P是线段AB上任意一点,在扇形COD的旋转过程中,请直接写出线段PC的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com