
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.则结论:①BE=EC;②∠EDC=∠ECD;③∠B=∠BDE;④△ABC∽△ACD;⑤△DEC是等边三角形.其中正确的结论有( )
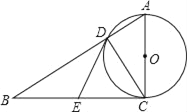
A. 2个 B. 3个 C. 4个 D. 5个
【答案】C
【解析】分析:连接OD,如图,先判断BC为⊙O的切线,再利用切线长定理得到ED=EC,则∠1=∠2,接着证明∠3=∠B得到ED=EB,从而得到EB=EC,即可判断①②③;根据相似三角形的判定即可判断④;根据等边三角形的判定即可判断⑤.
详解:连接OD,如图,
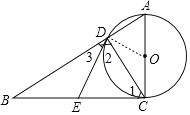
∵∠ACB=90°,
∴BC为⊙O的切线,
∵DE为切线,
∴ED=EC,
∴∠1=∠2,即∠EDC=∠ECD,∴②正确;
∵AC为直径,
∴∠ADC=90°,
∴∠2+∠3=90°,∠B+∠1=90°,
∴∠3=∠B,即∠B=∠BDE,∴③正确;
∴ED=EB,
∴EB=EC,∴①正确;
即点E是边BC的中点,
∵AC为直径,
∴∠ADC=90°=∠ACD,
∵∠A=∠A,
∴△ABC∽△ACD,∴④正确;
根据已知不能推出DC=DE=EC,即△DEC不一定是等边三角形,∴⑤错误;
即正确的个数是4个,
故选:C.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】某商场销售一种西装和领带,西装每套定价200元,领带每条定价40元.国庆节期间商场决定开展促销活动,活动期间向客户提供两种优惠方案:
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x![]() .
.
(1)若该客户按方案一购买,需付款多少元(用含x的式子表示)?若该客户按方案二购买,需付款多少元(用含x的式子表示)?
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算;
,通过计算说明此时按哪种方案购买较为合算;
(3)当![]() 时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在体育活动课中,体育老师随机抽取了九年级甲、乙两班部分学生进行某体育项目的测试,并对成绩进行统计分析,绘制了频数分布表,请你根据表中的信息完成下列问题:
(1)频数分布表中a= ,b= ;
(2)如果该校九年级共有学生900人,估计该校该体育项目的成绩为良和优的学生有多少人?
(3)已知第一组中有两个甲班学生,第二组中只有一个乙班学生,老师随机从这两个组中各选一名学生对体育活动课提出建议,则所选两人正好是甲班和乙班各一人的概率是多少?
分 组 | 频数 | 频率 |
第一组(不及格) | 3 | 0.15 |
第二组(中) | b | 0.20 |
第三组(良) | 7 | 0.35 |
第四组(优) | 6 | a |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,先阅读再解决后面的问题:
原题:如图1,点E,F分别在正方形ABCD的边BC,CD上,![]() ,连接EF,求证:EF=BE+DF.
,连接EF,求证:EF=BE+DF.
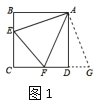
解题由于AB=AD,我们可以延长CD到点G,使DG=BE,易得![]() ,可证
,可证![]() .再证明
.再证明![]() ,得EF=FG=DG+FD=BE+DF.
,得EF=FG=DG+FD=BE+DF.
问题(1):如图2,在四边形ABCD中,AB=AD,![]() ,E,F分别是边BC,CD上的点,且
,E,F分别是边BC,CD上的点,且![]() ,求证:EF=BE+FD;
,求证:EF=BE+FD;

问题(2):如图3,在四边形ABCD中,![]() ,
,![]() ,AB=AD=1,点E,F分别在四边形ABCD的边BC,CD上的点,且
,AB=AD=1,点E,F分别在四边形ABCD的边BC,CD上的点,且![]() ,求此时
,求此时![]() 的周长
的周长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为任意三角形,以AB、AC为边分别向外做等边△ABD和等边△ACE,连接CD、BE并相交于点P.求证:
(1)CD=BE;
(2)∠BPC=120°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是杨辉三角系数表,它的作用是指导读者按规律写出行如(a+b)![]() 展开式的系数,请你仔细观察下表中的规律,填出展开式中所缺的系数。
展开式的系数,请你仔细观察下表中的规律,填出展开式中所缺的系数。
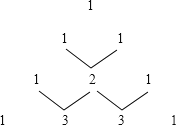
(1)、(a+b)=a+b
(2)、(a+b)![]() =a
=a![]() +2ab+b
+2ab+b![]()
(3)、(a+b) ![]() =a
=a![]() +3a
+3a![]() b+3ab
b+3ab![]() +b
+b![]()
(4)、(a+b)![]() =a
=a![]() + a
+ a![]() b+6a
b+6a![]() b
b![]() +4ab
+4ab![]() +b
+b![]()
(5)(a+b)![]() =a
=a![]() + a
+ a![]() b+ a
b+ a![]() b
b![]() + a
+ a![]() b
b![]() + ab
+ ab![]() +b
+b![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角△ABC中,AD是高,E,F分别是AB,AC中点,EF交AD于G,已知GF=1,AC= 6,△DEG的周长为10,则△ABC的周长为( )

A. 27-3![]() B. 28-3
B. 28-3![]() C. 28-4
C. 28-4![]() D. 29-5
D. 29-5![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
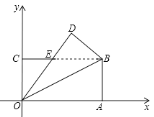
【题目】如图,矩形OABC的顶点与坐标原点O重合,将△OAB沿对角线OB所在的直线翻折,点A落在点D处,OD与BC相交于点E,已知OA=8,AB=4
(1)求证:△OBE是等腰三角形;
(2)求E点的坐标;
(3)坐标平面内是否存在一点P,使得以B,D,E,P为顶点的四边形是平行四边形?若存在,请直接写出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD.
(1)若∠AOC=70°,求∠DOE和∠EOF的度数;
(2)请写出图中∠AOD的补角和∠AOE的余角.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com