
【题目】如图,△ABC为任意三角形,以AB、AC为边分别向外做等边△ABD和等边△ACE,连接CD、BE并相交于点P.求证:
(1)CD=BE;
(2)∠BPC=120°.

【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)根据等边三角形的性质得出AD=AB,AE=AC,∠ACE=∠AEC=60°,∠DAB=∠EAC=60°,求出∠DAC=∠BAE,根据SAS推出△DAC≌△BAE即可;
(2)根据全等三角形的性质得出∠BEA=∠ACD,求出∠BPC=∠ECP+∠PEC=∠ACE+∠AEC,代入求出即可.
试题解析:(1)∵以AB、AC为边分别向外做等边△ABD和等边△ACE,
∴AD=AB,AE=AC,∠ACE=∠AEC=60°,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中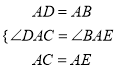 ,
,
∴△DAC≌△BAE(SAS),
∴CD=BE;
(2)∵△DAC≌△BAE,
∴∠BEA=∠ACD,
∴∠BPC=∠ECP+∠PEC=∠DCA+∠ACE+∠PEC=∠BEA+∠ACE+∠PEC=∠ACE+∠AEC=60°+60°=120°.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
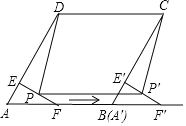
【题目】如图,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点,过点F作FE⊥AD,垂足为E,将△AEF沿点A到点B的方向平移,得到△A′E′F′.
(1)求EF的长;
(2)设P,P′分别是EF,E′F′的中点,当点A′与点B重合时,求证四边形PP′CD是平行四边形,并求出四边形PP′CD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
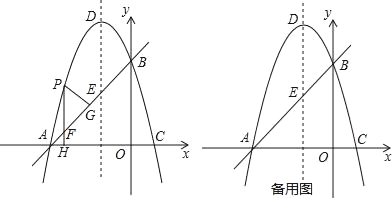
【题目】如图,在平面直角坐标系xoy中,直线y=x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线y=﹣x2+bx+c交x轴于另一点C,点D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)点P是直线AB上方的抛物线上一点,(不与点A、B重合),过点P作x轴的垂线交x轴于点H,交直线AB于点F,作PG⊥AB于点G.求出△PFG的周长最大值;
(3)在抛物线y=﹣x2+bx+c上是否存在除点D以外的点M,使得△ABM与△ABD的面积相等?若存在,请求出此时点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB⊥BC,CD⊥BC,垂足分别为B、C,AB=BC,E为BC的中点,且AE⊥BD于F,若CD=4cm,则AB的长度为( )

A. 4cm B. 8cm C. 9cm D. 10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰直角△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)求证:△ADC≌△CEB;
(2)求证:AD+BE=DE;
(3)当直线MN绕点C旋转到图2的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
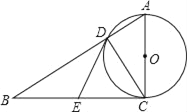
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.则结论:①BE=EC;②∠EDC=∠ECD;③∠B=∠BDE;④△ABC∽△ACD;⑤△DEC是等边三角形.其中正确的结论有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知□ABCD的面积为100,P为边CD上的任一点,E,F分别为线段AP,BP的中点,则图中阴影部分的总面积为( )

A. 30B. 25C. 22.5D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】华为手机新款上市,十分畅销.某经销商进价每台3000元,售价每台4000 元.一月份销量为512台,二、三月份销量持续走高,三月份销量达到800台.
(1)求二、三月份每月销量的平均增长率;
(2)根据市场调查经验,四月份此款手机销售情况将不再火爆而是趋于平稳.若售价不变,四月份销量将与三月份持平;若降价促销,每台每降价50元,月销量将增加100台.要使四月份利润达到90万元,每台应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com