
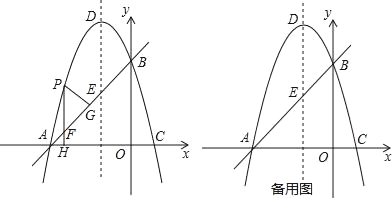
【题目】如图,在平面直角坐标系xoy中,直线y=x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线y=﹣x2+bx+c交x轴于另一点C,点D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)点P是直线AB上方的抛物线上一点,(不与点A、B重合),过点P作x轴的垂线交x轴于点H,交直线AB于点F,作PG⊥AB于点G.求出△PFG的周长最大值;
(3)在抛物线y=﹣x2+bx+c上是否存在除点D以外的点M,使得△ABM与△ABD的面积相等?若存在,请求出此时点M的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2﹣2x+3;(2)![]() ,(3)M1(﹣2,3),M2(
,(3)M1(﹣2,3),M2(![]() ,
,![]() ),M3(
),M3(![]() ,
,![]() ).
).
【解析】试题分析:(1)将已知点的坐标代入二次函数的解析式利用待定系数法确定二次函数的解析式即可;
(2)首先根据△PFG是等腰直角三角形,设P(m,-m2-2m+3)得到F(m,m+3),进而得到PF=-m2-2m+3-m-3=-m2-3m,从而得到△PFG周长为:-m2-3m+![]() (-m2-3m),配方后即可确定其最大值;
(-m2-3m),配方后即可确定其最大值;
(3)当DM1∥AB,M3M2∥AB,且与AB距离相等时,根据同底等高可以确定△ABM与△ABD的面积相等,分别求得直线DM1解析式为:y=x+5和直线M3M2解析式为:y=x+1,联立之后求得交点坐标即可.
试题解析:(1)∵直线AB:y=x+3与坐标轴交于A(-3,0)、B(0,3),
代入抛物线解析式y=-x2+bx+c中,得:
![]() ,
,
∴![]()
∴抛物线解析式为:y=-x2-2x+3;
(2)∵由题意可知△PFG是等腰直角三角形,
设P(m,-m2-2m+3),
∴F(m,m+3),
∴PF=-m2-2m+3-m-3=-m2-3m,
△PFG周长为:-m2-3m+![]() (-m2-3m),
(-m2-3m),
=-(![]() +1)(m+
+1)(m+![]() )2+
)2+![]() ,
,
∴△PFG周长的最大值为:![]() .
.
(3)点M有三个位置,如图所示的M1、M2、M3,都能使△ABM的面积等于△ABD的面积.
此时DM1∥AB,M3M2∥AB,且与AB距离相等,
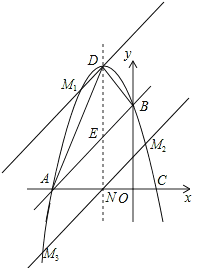
∵D(-1,4),
∴E(-1,2)、则N(-1,0)
∵y=x+3中,k=1,
∴直线DM1解析式为:y=x+5,
直线M3M2解析式为:y=x+1,
∴x+5=-x2-2x+3或x+1=-x2-2x+3,
∴x1=-1,x2=-2,x3=![]() ,x4=
,x4=![]() ,
,
∴M1(-2,3),M2(![]() ,
,![]() ),M3(
),M3(![]() ,
,![]() ).
).


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
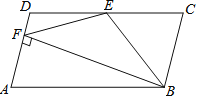
【题目】如图,在平行四边形ABCD中,AB=2AD,BE平分∠ABC交CD于点E,作BF⊥AD,垂足为F,连接EF,小明得到三个结论:①∠FBC=90°;②ED=EB;③S△EBF=S△EDF+S△EBC;则三个结论中一定成立的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,P是BC边上一动点(点P不与B、C重合),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA、NA,则以下结论:①△CMP∽△BPA;②四边形AMCB的面积最大值为2.5;③△ADN≌△AEN;④线段AM的最小值为2.5;⑤当P为BC中点时,AE为线段NP的中垂线.正确的有_____(只填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂计划平均每天生产200辆,但是由于种种原因,实际每天生产量与计划量相比有出入。表是某周的生产情况(超产记为正,减产记为负):

(1)根据记录的数据可知该厂星期三生产自行车多少辆?
(2)产量最多的一天比产量最少的一天多生产自行车多少辆?
(3)根据记录的数据可知该厂本周实际共生产自行车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
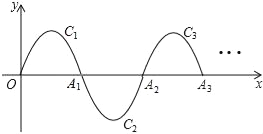
【题目】如图,一段抛物线y=﹣x(x﹣5)(0≤x≤5),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,得到一“波浪线”,若点P(2018,m)在此“波浪线”上,则m的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在体育活动课中,体育老师随机抽取了九年级甲、乙两班部分学生进行某体育项目的测试,并对成绩进行统计分析,绘制了频数分布表,请你根据表中的信息完成下列问题:
(1)频数分布表中a= ,b= ;
(2)如果该校九年级共有学生900人,估计该校该体育项目的成绩为良和优的学生有多少人?
(3)已知第一组中有两个甲班学生,第二组中只有一个乙班学生,老师随机从这两个组中各选一名学生对体育活动课提出建议,则所选两人正好是甲班和乙班各一人的概率是多少?
分 组 | 频数 | 频率 |
第一组(不及格) | 3 | 0.15 |
第二组(中) | b | 0.20 |
第三组(良) | 7 | 0.35 |
第四组(优) | 6 | a |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,△ADC和△BDE均为等腰三角形,∠CAD=∠DBE,AC=AD,BD=BE,连接CE,点G为CE的中点,过点E作AC的平行线与线段AG延长线交于点F.
(1)当A,D,B三点在同一直线上时(如图1),求证:G为AF的中点;
(2)将图1中△BDE绕点D旋转到图2位置时,点A,D,G,F在同一直线上,点H在线段AF的延长线上,且EF=EH,连接AB,BH,试判断△ABH的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为任意三角形,以AB、AC为边分别向外做等边△ABD和等边△ACE,连接CD、BE并相交于点P.求证:
(1)CD=BE;
(2)∠BPC=120°.

查看答案和解析>>
科目:初中数学 来源: 题型:
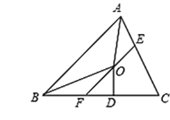
【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于点F,交AC于点E,过点O作OD⊥BC于D,下列四个结论:①∠AOB=90°+![]() ∠C;②AE+BF=EF;③当∠C=90°时,E、F分别是AC、BC的中点;④若OD=
∠C;②AE+BF=EF;③当∠C=90°时,E、F分别是AC、BC的中点;④若OD=![]() CE+CF=
CE+CF=![]() 则S△CEF=
则S△CEF=![]() ,其中正确的是______________
,其中正确的是______________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com