
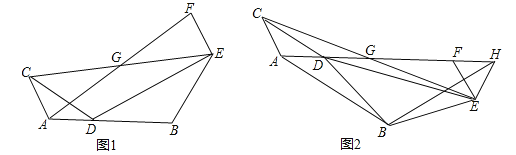
����Ŀ����֪��ͼ����ADC����BDE��Ϊ���������Σ���CAD=��DBE��AC=AD��BD=BE������CE����GΪCE���е㣬����E��AC��ƽ�������߶�AG�ӳ��߽��ڵ�F��
��1����A��D��B������ͬһֱ����ʱ����ͼ1������֤��GΪAF���е㣻
��2����ͼ1����BDE�Ƶ�D��ת��ͼ2λ��ʱ����A��D��G��F��ͬһֱ���ϣ���H���߶�AF���ӳ����ϣ���EF=EH������AB��BH�����ж���ABH����״����˵�����ɣ�

���𰸡���1��֤������������2����ABHΪ���������Σ����ɼ�����.
�������������������1������AC��EF���ɵ���ACG=��FEG�����ݵ�GΪCE���е����ɵ�CG=EG���ٸ�����AGC=��FGE�����ɵó���ACG�ա�FEG�������õ�GΪAF���е���
��2��������ACG�ա�FEG���ɵ�AC=FE���ٸ���AC=AD��FE=HE�����ɵõ�AD=HE�������ı����ڽǺ��Լ�ͬ�ǵIJ�����ȿɵ���BEH=��BDA���ٸ���BD=BE�����ɵõ���ADB�ա�HEB���ɵ�AB=HB������ABH�ǵ��������Σ�
���������������1����AC��EF�����ACG=��FEG���ߵ�GΪCE���е�����CG=EG���֡���AGC=��FGE�����ACG�ա�FEG����AG=FG����GΪAF���е���
��2����ABH��������������������
ͬ��1����֤��ACG�ա�FEG����AC=FE���֡�AC=AD��FE=HE����AD=HE����
��AC��EF�����GFE=��CAD=��DBE����EF=EH�����EFH=��EHF������EFH+��GFE=180�㣬���FHE+��DBE=180�㣬���ı���BDHE������BEH+��BDF=180�����֡���BDA+��BDF=180�㣬���BEH=��BDA����
����BD=BE����
�����٢ڢۣ��ɵ���ADB�ա�HEB����AB=HB������ABH�ǵ��������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��C��D�����߶�ABΪֱ���ġ�O�����㣬��CA=CD���ҡ�ACD=30�㣬���CAB=�� �� 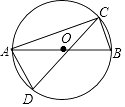
A.15��
B.20��
C.25��
D.30��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����������ο�������߳��ֱ�Ϊ24cm��30cm��36cm��Ҫ����һ���������Ƶ����������ο�ܣ����г�Ϊ27cm��45cm���������ģ�Ҫ�������е�һ��Ϊһ�ߣ�����һ���Ͻ������Σ����������ϣ���Ϊ�������ߣ��ط��У� ��
A.0��
B.1��
C.2��
D.3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���۲�����ͼ�����ʽ�Ĺ�ϵ������գ�
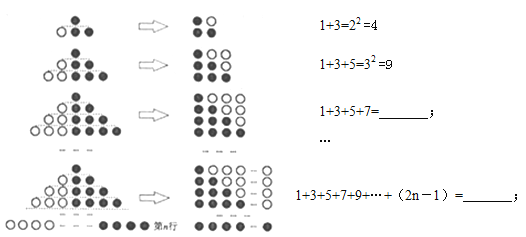
��2��������1���н��ۣ��������������
��1+3+5+��+203=�� ����
��������101+103+105+��+199��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A1A2=1����OA1A2=90�㣬��A1OA2=30������б��OA2Ϊֱ�DZ���ֱ�������Σ�ʹ�á�A2OA3=30����������ǰһ��ֱ�������ε�б��Ϊֱ�DZ�һֱ����30���ǵ�ֱ�������Σ���Rt��A2014OA2015�����Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��һ�����ڵĵ�A�ڷ���������y= ![]() ��ͼ���ϣ��ڶ������ڵĵ�B�ڷ���������y=
��ͼ���ϣ��ڶ������ڵĵ�B�ڷ���������y= ![]() ��ͼ���ϣ���OA��OB��cosA=
��ͼ���ϣ���OA��OB��cosA= ![]() ����k��ֵΪ�� ��
����k��ֵΪ�� ��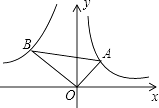
A.��3
B.��4
C.�� ![]()
D.��2 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���ֱ�ǡ�ABC�У���ACB��90�㣬O��б��AB���е㣬��D��E�ֱ���ֱ�DZ�AC��BC�ϣ��ҡ�DOE��90�㣬DE��OC�ڵ�P�������н��ۣ���ͼ����ȫ�ȵ�������ֻ�����ԣ��ڡ�ABC����������ı���CDOE���������������CD��CE��![]() OA����AD2��BE2��DE2.������ȷ�Ľ�����( )
OA����AD2��BE2��DE2.������ȷ�Ľ�����( )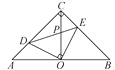
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����˾����ʦ��ij������Ӫ��ȫ���ڶ�����ij���·�Ͻ��еģ������Ϊ��������Ϊ���������������г���̣���λ��km�����£�
![]() .
.
��.���һ���˿��͵�Ŀ�ĵأ�����ڶ��滹�����棿�ڶ���ǧ�״���
��.�������ʦ����һ�£�����������һ����ʻ�˶�����̣�
��.��ÿǧ����0.1L��������������ʦ��һ�����˶������ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����9�֣�̽���⣺��ͼ��
��1����ABCΪ�ȱ������Σ�����D�ڱ�CA�ϣ�����P����BC�ϣ���������ֱ��C��B��ͬʱ����������ͬ���ٶ���C��A����B��C�˶�������AP��BD���ڵ�Q�������˶�������AP=BD��������֤����Ľ��ۣ�
��2�������ԭ���С�����D�ڱ�CA�ϣ�����P��BC�ϣ�����Ϊ������D��P������CA������BC���˶�����������
�����䣬��ͼ��2����ʾ�������˶���������BQP�Ĵ�С���ֲ��䣮��������ͼ��2�������Σ�
��֤����BQP=60�㣻
��3�������ԭ���С�����P�ڱ�BC�ϡ���Ϊ������P��AB���ӳ������˶�������PD��BC��E���������������䣬��ͼ��3������D��P���˶������У�DEʼ�յ���PE��д��֤�����̣�
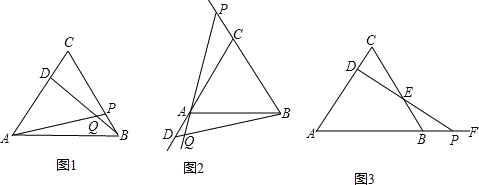
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com