
����Ŀ����9�֣�̽���⣺��ͼ��
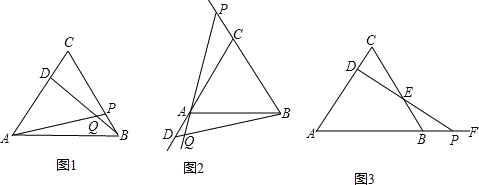
��1����ABCΪ�ȱ������Σ�����D�ڱ�CA�ϣ�����P����BC�ϣ���������ֱ��C��B��ͬʱ����������ͬ���ٶ���C��A����B��C�˶�������AP��BD���ڵ�Q�������˶�������AP=BD��������֤����Ľ��ۣ�
��2�������ԭ���С�����D�ڱ�CA�ϣ�����P��BC�ϣ�����Ϊ������D��P������CA������BC���˶�����������
�����䣬��ͼ��2����ʾ�������˶���������BQP�Ĵ�С���ֲ��䣮��������ͼ��2�������Σ�
��֤����BQP=60�㣻
��3�������ԭ���С�����P�ڱ�BC�ϡ���Ϊ������P��AB���ӳ������˶�������PD��BC��E���������������䣬��ͼ��3������D��P���˶������У�DEʼ�յ���PE��д��֤�����̣�
���𰸡���1����2����������3��DE=PE
��������
������1������ABCΪ�ȱ������Σ��ɵ���C=��ABP=60�㣬AB=BC������������ֱ��C��B��ͬʱ����������ͬ���ٶ���C��A����B��C�˶����ɵ�BP=CD����������SAS���ж���ABP�ա�BCD���̶�֤�ý��ۣ�
��2��ͬ����֤����ABP�ա�BCD��SAS������ɵ���APB=��BDC��Ȼ������APB+��PAC=��ACB=60�㣬��DAQ=��PAC�������BDC+��DAQ=��BQP=60�㣻
��3�����ȹ���D��DG��AB��BC�ڵ�G�����֤����DCGΪ�ȱ������Σ��̶�֤����DGE�ա�PBE��AAS�������֤�ý��ۣ�
����������⣺��1��������
���ɣ��ߡ�ABC�ǵȱ������Σ�
���C=��ABP=60�㣬AB=BC��
��������ã�CD=BP��
����ABP����BCD��
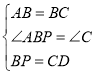 ��
��
���ABP�ա�BCD��SAS����
��AP=BD��
��2���������⣬CP=AD��
��CP+BC=AD+AC��
��BP=CD��
����ABP����BCD��
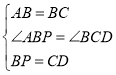 ��
��
���ABP�ա�BCD��SAS����
���APB=��BDC��
�ߡ�APB+��PAC=��ACB=60�㣬��DAQ=��PAC��
���BDC+��DAQ=��BQP=60�㣻
��3��DE=PE��
���ɣ�����D��DG��AB��BC�ڵ�G��
���CDG=��C=��CGD=60�㣬��GDE=��BPE��
���DCGΪ�ȱ������Σ�
��DG=CD=BP��
����DGE����PBE��
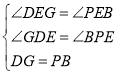 ��
��
���DGE�ա�PBE��AAS����
��DE=PE��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ����ADC����BDE��Ϊ���������Σ���CAD=��DBE��AC=AD��BD=BE������CE����GΪCE���е㣬����E��AC��ƽ�������߶�AG�ӳ��߽��ڵ�F��
��1����A��D��B������ͬһֱ����ʱ����ͼ1������֤��GΪAF���е㣻
��2����ͼ1����BDE�Ƶ�D��ת��ͼ2λ��ʱ����A��D��G��F��ͬһֱ���ϣ���H���߶�AF���ӳ����ϣ���EF=EH������AB��BH�����ж���ABH����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=kx+3��x�ᣬy��ֱ���A��B���㣬tan��OAB= ![]() ����C��x��y����ֱ��y=kx+3����A��B���غϵĶ��㣮
����C��x��y����ֱ��y=kx+3����A��B���غϵĶ��㣮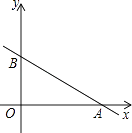
��1����ֱ��y=kx+3�Ľ���ʽ��
��2������C�˶���ʲôλ��ʱ��AOC�������6��
��3������C����һֱ��CD��y���ཻ��D�㣬�Ƿ���ڵ�Cʹ��BCD���AOB���ƣ��ҡ�BCD������ǡ�AOB������� ![]() �������ڣ��������C�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ��������C�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB��90������D��E�ֱ���AB��AC�ϣ�CE��BC������CD�����߶�CD�Ƶ�C��˳ʱ�뷽����ת90�����CF������EF. ��EF��CD����֤����BDC��90��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ���뷴��������y= ![]() ��ͼ���ڵ�A����2����5 ����C ��5��n������y���ڵ�B����x���ڵ�D����ô����ʽkx+b��
��ͼ���ڵ�A����2����5 ����C ��5��n������y���ڵ�B����x���ڵ�D����ô����ʽkx+b�� ![]() ��0�Ľ⼯�� ��
��0�Ľ⼯�� �� 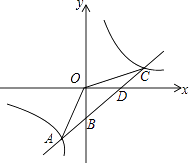
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬B��x���ϣ��ı���OACBΪƽ���ı��Σ���
��AOB=60�㣬����������![]() ��k��0���ڵ�һ�����ڹ���A������BC���ڵ�F����FΪBC���е㣬��S��AOF��12
��k��0���ڵ�һ�����ڹ���A������BC���ڵ�F����FΪBC���е㣬��S��AOF��12![]() ʱ��OA�ij�Ϊ____.
ʱ��OA�ij�Ϊ____.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������������y= ![]() ��ͼ����һ�κ���y=x+b��ͼ���ڵ�A��1��4������B����4��n����
��ͼ����һ�κ���y=x+b��ͼ���ڵ�A��1��4������B����4��n���� 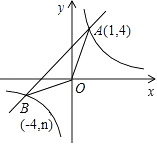
��1����һ�κ����ͷ����������Ľ���ʽ��
��2�����OAB�������
��3��ֱ��д��һ�κ���ֵ���ڷ���������ֵ���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ȱ���ABC�ı߳�Ϊ4�� P��Q��R�ֱ�Ϊ��AB��BC��AC�ϵĶ��㣬��PR��QR����Сֵ�� _____.
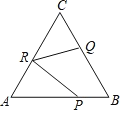
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������꼶����������ʵ����ijɼ������������ֳ�5��С�飨x��ʾ�ɼ�����λ���ף���A�飺5.25��x��6.25��B�飺6.25��x��7.25��C�飺7.25��x��8.25��D�飺8.25��x��9.25��E�飺9.25��x��10.25�������Ƴ�����ͳ��ͼ��Ƶ���ֲ�ֱ��ͼ�������������涨x��6.25Ϊ�ϸ�x��9.25Ϊ���㣮
��1���ⲿ�������ж����ˣ����гɼ��ϸ���ж����ˣ�
��2���ⲿ�������ɼ�����λ��������һ�飿����ͳ��ͼ��D���Ӧ��Բ�Ľ��Ƕ��ٶȣ�
��3��Ҫ�ӳɼ������ѧ���У����ѡ��2�˽��ܾ��飬��֪�ס�����λͬѧ�ijɼ���Ϊ���㣬������������1�˱�ѡ�еĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com