
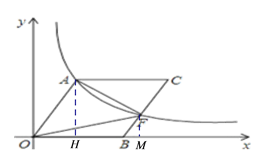
【题目】在平面直角坐标系中,O为坐标原点,B在x轴上,四边形OACB为平行四边形,且
∠AOB=60°,反比例函数![]() (k>0)在第一象限内过点A,且与BC交于点F。当F为BC的中点,且S△AOF=12
(k>0)在第一象限内过点A,且与BC交于点F。当F为BC的中点,且S△AOF=12![]() 时,OA的长为____.
时,OA的长为____.

【答案】8
【解析】分析:
过点A作AH⊥OB于点H,过点F作FM⊥OB于点M,设OA=x,在由已知易得:AH=![]() ,OH=
,OH=![]() ,由此可得S△AOH=
,由此可得S△AOH=![]() 由点F是平行四边形AOBC的BC边上的中点,可得BF=
由点F是平行四边形AOBC的BC边上的中点,可得BF=![]() ,BM=
,BM=![]() ,FM=
,FM=![]() ,由此可得S△BMF=
,由此可得S△BMF=![]() ,由S△OAF=
,由S△OAF=![]() 可得S△OBF=
可得S△OBF=![]() ,由此可得S△OMF=
,由此可得S△OMF=![]() ,由点A、F都在反比例函数
,由点A、F都在反比例函数![]() 的图象上可得S△AOH=S△BMF,由此即可列出关于x的方程,解方程即可求得OA的值.
的图象上可得S△AOH=S△BMF,由此即可列出关于x的方程,解方程即可求得OA的值.
详解:
如下图,点A作AH⊥OB于点H,过点F作FM⊥OB于点M,设OA=x,
∵四边形AOBC是平行四边形,∠AOB=60°,点F是BC的中点,S△OAF=![]() ,
,
∴AH=![]() ,OH=
,OH=![]() ,BF=
,BF=![]() ,∠FBM=60°,S△OBF=
,∠FBM=60°,S△OBF=![]() ,
,
∴S△AOH=![]() ,BM=
,BM=![]() ,FM=
,FM=![]() ,
,
∴S△BMF=![]() ,
,
∴S△OMF=![]() ,
,
∵由点A、F都在反比例函数![]() 的图象上,
的图象上,
∴S△AOH=S△BMF,
∴![]() =
=![]() ,
,
化简得:![]() ,解得:
,解得:![]() (不合题意,舍去),
(不合题意,舍去),
∴OA=8.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知第一象限内的点A在反比例函数y= ![]() 的图象上,第二象限内的点B在反比例函数y=
的图象上,第二象限内的点B在反比例函数y= ![]() 的图象上,且OA⊥OB,cosA=
的图象上,且OA⊥OB,cosA= ![]() ,则k的值为( )
,则k的值为( )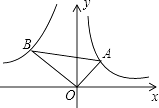
A.﹣3
B.﹣4
C.﹣ ![]()
D.﹣2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
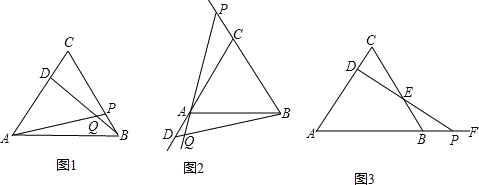
【题目】(9分)探究题:如图:
(1)△ABC为等边三角形,动点D在边CA上,动点P在边BC上,若这两点分别从C、B点同时出发,以相同的速度由C向A和由B向C运动,连接AP,BD交于点Q,两点运动过程中AP=BD成立吗?请证明你的结论;
(2)如果把原题中“动点D在边CA上,动点P边BC上,”改为“动点D,P在射线CA和射线BC上运动”,其他条
件不变,如图(2)所示,两点运动过程中∠BQP的大小保持不变.请你利用图(2)的情形,
求证:∠BQP=60°;
(3)如果把原题中“动点P在边BC上”改为“动点P在AB的延长线上运动,连接PD交BC于E”,其他条件不变,如图(3),则动点D,P在运动过程中,DE始终等于PE吗?写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=﹣ ![]() x2+bx+c与x轴交于A,B两点,其中B(6,0),与y轴交于点C(0,8),点P是x轴上方的抛物线上一动点(不与点C重合).
x2+bx+c与x轴交于A,B两点,其中B(6,0),与y轴交于点C(0,8),点P是x轴上方的抛物线上一动点(不与点C重合).
(1)求抛物线的表达式;
(2)过点P作PD⊥x轴于点D,交直线BC于点E,点E关于直线PC的对称点为E′,若点E′落在y轴上(不与点C重合),请判断以P,C,E,E′为顶点的四边形的形状,并说明理由;
(3)在(2)的条件下直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村计划对总长为1800m的道路进行改造,安排甲、乙两个工程队完成.已知甲队每天能完成的道路长度是乙队每天能完成的2倍,并且在独立完成长为400m的道路时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成道路的长度分别是多少m?
(2)若村委每天需付给甲队的道路改造费用为0.4万元,乙队为0.25万元,要使这次的道路改造费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“摩拜单车”公司调查无锡市民对其产品的了解情况,随机抽取部分市民进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为![]() 、
、![]() 、
、![]() 、
、![]() .根据调查结果绘制了如下尚不完整的统计图.
.根据调查结果绘制了如下尚不完整的统计图.
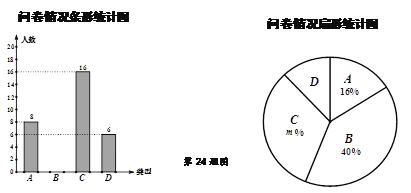
(1)本次问卷共随机调查了 名市民,扇形统计图中![]() .
.
(2)请根据数据信息补全条形统计图.
(3)扇形统计图中“D类型”所对应的圆心角的度数是 .
(4)从这次接受调查的市民中随机抽查一个,恰好是“不了解”的概率是 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列一组勾股数:
|
|
| |
第1组 | 3=2×1+1 | 4=2×1×(1+1) | 5=2×1×(1+1)+1 |
第2组 | 5=2×2+1 | 12=2×2×(2+1) | 13=2×2×(2+1)+1 |
第3组 | 7=2×3+1 | 24=2×3×(3+1) | 25=2×3×(3+1)+1 |
第4组 | 9=2×4+1 | 40=2×4×(4+1) | 41=2×4×(4+1)+1 |
… | … | … | … |
观察以上各组勾股数的特点:
(1)请写出第7组勾股数![]() ,
,![]() ,
,![]() ;
;
(2)写出第![]() 组勾股数
组勾股数![]() ,
,,
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com