
����Ŀ�������꼶����������ʵ����ijɼ������������ֳ�5��С�飨x��ʾ�ɼ�����λ���ף���A�飺5.25��x��6.25��B�飺6.25��x��7.25��C�飺7.25��x��8.25��D�飺8.25��x��9.25��E�飺9.25��x��10.25�������Ƴ�����ͳ��ͼ��Ƶ���ֲ�ֱ��ͼ�������������涨x��6.25Ϊ�ϸ�x��9.25Ϊ���㣮
��1���ⲿ�������ж����ˣ����гɼ��ϸ���ж����ˣ�
��2���ⲿ�������ɼ�����λ��������һ�飿����ͳ��ͼ��D���Ӧ��Բ�Ľ��Ƕ��ٶȣ�
��3��Ҫ�ӳɼ������ѧ���У����ѡ��2�˽��ܾ��飬��֪�ס�����λͬѧ�ijɼ���Ϊ���㣬������������1�˱�ѡ�еĸ��ʣ�
���𰸡�
��1��
�⣺��A��ռ10%����5�ˣ�
���ⲿ���������У�5��10%=50���ˣ���
��ֻ��A��5�˳ɼ����ϸ�
��ϸ�����Ϊ��50��5=45���ˣ���
��2��
�⣺��C��ռ30%������������50��30%=15���ˣ���B����10�ˣ�D����15�ˣ�
����50�������ijɼ��ɵ͵��߷�������A����5�ˣ�B����10�ˣ�C����15�ˣ�D����15�ˣ�E����5�ˣ�
��ɼ�����λ������C�飻
��D����15�ˣ�ռ15��50=30%��
���Ӧ��Բ�Ľ�Ϊ��360���30%=108�㣻
��3��
�⣺�ɼ������������E�飬���ס���������������������������Ϊa��b��c��
����״ͼ�ã�
�߹���20�ֵȿ��ܵĽ��������������1�˱�ѡ�е���14�������
������������1�˱�ѡ�еĸ���Ϊ�� ![]() =
= ![]() ��
��
����������1�����ݡ����֡°ٷֱ�=������������������ٸ�������ò��ϸ�ķ������Ӷ�֪A��Ϊ���ϸ�ķ�����
��2��һ�����ݴ�С�����˳�����У��������м��������λ����Բ�ĽǶ���=360����ٷֱȣ�
��3�����б�������״ͼ���г����еȿ��ܵĽ�������ҳ��¼����ֵĽ�������Ӷ��ø��ʹ�ʽ������� .


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����9�֣�̽���⣺��ͼ��
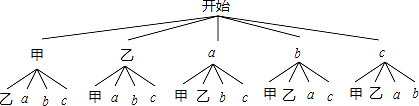
��1����ABCΪ�ȱ������Σ�����D�ڱ�CA�ϣ�����P����BC�ϣ���������ֱ��C��B��ͬʱ����������ͬ���ٶ���C��A����B��C�˶�������AP��BD���ڵ�Q�������˶�������AP=BD��������֤����Ľ��ۣ�
��2�������ԭ���С�����D�ڱ�CA�ϣ�����P��BC�ϣ�����Ϊ������D��P������CA������BC���˶�����������
�����䣬��ͼ��2����ʾ�������˶���������BQP�Ĵ�С���ֲ��䣮��������ͼ��2�������Σ�
��֤����BQP=60�㣻
��3�������ԭ���С�����P�ڱ�BC�ϡ���Ϊ������P��AB���ӳ������˶�������PD��BC��E���������������䣬��ͼ��3������D��P���˶������У�DEʼ�յ���PE��д��֤�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
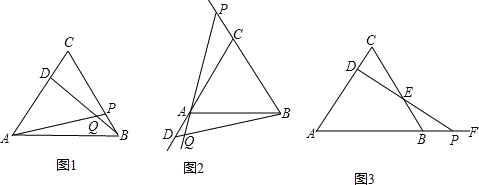
����Ŀ����ͼ��ij���ʵ���С��ʵ�ز�����������ƽ�е�һ�κӵĿ��ȣ��ںӵ��ϰ��ߵ�A������úӵı����ߵ�B���䱱ƫ��45�㷽��Ȼ��������60m����C�㣬��õ�B�ڵ�C�ı�ƫ��60�㷽�ش��������⣺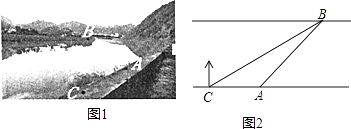
��1����CBA�Ķ���Ϊ ��
��2�������κӵĿ��������ȷ��1m���������� ![]() ��1.41��
��1.41�� ![]() ��1.73��
��1.73��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����P��ƽ���ı���ABCD�Խ���AC����ֱ���ϵ�һ�����㣨��P�����A��C�غϣ����ֱ����A��C��ֱ��BP�����ߣ�����ֱ�ΪE��F����OΪAC���е㣮
��1������P���O�غ�ʱ��ͼ1����֤��OE=OF
��2��ֱ��BP�Ƶ�B��ʱ�뷽����ת������P�ڶԽ���AC��ʱ���ҡ�OFE=30��ʱ����ͼ2�������߶�CF��AE��OE֮����������������ϵ��������֤����
��3������P�ڶԽ���CA���ӳ�����ʱ���ҡ�OFE=30��ʱ����ͼ3�������߶�CF��AE��OE֮����������������ϵ��ֱ��д�����ۼ��ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC=90�㣬D��E�ֱ���BC��AC�ϣ�AD��DE����AD=DE����F��AE���е㣬FD��AB�ཻ�ڵ�M��
��1����֤����FMC=��FCM��
��2��AD��MC��ֱ�𣿲�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�����һ�鹴������
|
|
| |
��1�� | 3=2��1+1 | 4=2��1����1+1�� | 5=2��1����1+1��+1 |
��2�� | 5=2��2+1 | 12=2��2����2+1�� | 13=2��2����2+1��+1 |
��3�� | 7=2��3+1 | 24=2��3����3+1�� | 25=2��3����3+1��+1 |
��4�� | 9=2��4+1 | 40=2��4����4+1�� | 41=2��4����4+1��+1 |
�� | �� | �� | �� |
�۲����ϸ��鹴�������ص㣺
��1����д����7�鹴����![]() ��
��![]() ��
��![]() ��
��
��2��д����![]() �鹴����
�鹴����![]() ��
����
![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������A���ʾ��![]() ��B���ʾ��
��B���ʾ��![]() ��
��![]() ��
��![]() ����|
����|![]() |+|
|+|![]() |=0��
|=0��
![]()
��1����A��ʾ����Ϊ_____����B��ʾ����Ϊ_____��
��2������ԭ��O����һ���壬һС��״ӵ�A����1����λ/����ٶ������˶���ͬʱ��һС���Ҵӵ�B����2����λ/����ٶ�Ҳ�����˶������������������Ĵ�С���ɿ���һ�㣩��ԭ�����ٶ����෴�ķ����˶������˶���ʱ��Ϊt���룩��
�ٵ�t=1ʱ����С��ԭ��ľ���=_____����С��ԭ��ľ���=_____.
��t=3ʱ����С��ԭ��ľ���=_____����С��ԭ��ľ���=_____.
����̽�����ף�����С��ԭ��ľ����������������ܣ���˵�����ɣ����ܣ���ֱ��д���ף�����С��ԭ��ľ������ʱ������ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��������OAB�У���AOB��90�㣬��A��60���xOA��30�㣬AB��y��Ľ�������DΪ��0��4������A��B������.
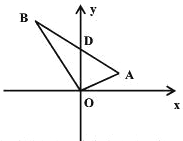
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ6��B����������A����һ�㣬��A��B�����ľ���Ϊ10������P�ӵ�A��������ÿ��6����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t��0���룮
��1�������ϵ�B��ʾ�������� ������P��ʾ�������� �����ú�t�Ĵ���ʽ��ʾ����
��2������Q�ӵ�B��������ÿ��4����λ���ȵ��ٶ����������������˶�������P��Qͬʱ��������
�ٵ���P�˶�������ʱ����P���Q������
�ڵ���P�˶�������ʱ����P���Q��ľ���Ϊ8����λ���ȣ�
![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com