
【题目】如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
(1)求证:∠FMC=∠FCM;
(2)AD与MC垂直吗?并说明理由.

【答案】(1)证明见解析;(2)AD⊥MC,理由见解析.
【解析】试题分析:(1)根据等腰直角三角形的性质得出DF⊥AE,DF=AF=EF,进而利用全等三角形的判定得出△DFC≌△AFM(AAS),即可得出答案;
(2)由(1)知,∠MFC=90°,FD=EF,FM=FC,即可得出∠FDE=∠FMC=45°,即可理由平行线的判定得出答案.
(1)证明:∵△ADE是等腰直角三角形,F是AE中点,
∴DF⊥AE,DF=AF=EF,
又∵∠ABC=90°,
∠DCF,∠AMF都与∠MAC互余,
∴∠DCF=∠AMF,
在△DFC和△AFM中,
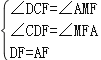 ,
,
∴△DFC≌△AFM(AAS),
∴CF=MF,
∴∠FMC=∠FCM;
(2)AD⊥MC,
理由:由(1)知,∠MFC=90°,FD=FA=FE,FM=FC,
∴∠FDE=∠FMC=45°,
∴DE∥CM,
∴AD⊥MC.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() 的图象交于点A(﹣2,﹣5 ),C (5,n),交y轴于点B,交x轴于点D,那么不等式kx+b﹣
的图象交于点A(﹣2,﹣5 ),C (5,n),交y轴于点B,交x轴于点D,那么不等式kx+b﹣ ![]() >0的解集是 .
>0的解集是 . 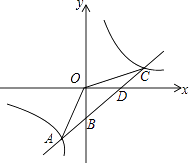
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直径坐标系中,反比例函数y= ![]() (x>0)的图象上有一点A(m,4),过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D,CD=
(x>0)的图象上有一点A(m,4),过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D,CD= ![]()
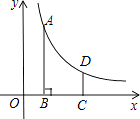
(1)点D的横坐标为(用含m的式子表示);
(2)求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AD平分∠BAC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.
(1)求证:四边形ADCE是矩形;
(2)当△ABC满足什么条件时,四边形ADCE是正方形?给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,∠ABC=2∠C,BE平分∠ABC交AC于E,AD⊥BE于D,下列结论:①AC﹣BE=AE;②点E在线段BC的垂直平分线上;③∠DAE=∠C;④BC=4AD,其中正确的有( )
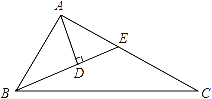
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.
(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了一次G20知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题: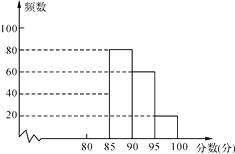
分数段 | 频数 | 频率 |
80≤x<85 | a | 0.2 |
85≤x<90 | 80 | b |
90≤x<95 | 60 | c |
95≤x<100 | 20 | 0.1 |
(1)求出表中a,b,c的数值,并补全频数分布直方图;
(2)获奖成绩的中位数落在哪个分数段?
(3)估算全体获奖同学成绩的平均分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面一列数,探求其规律:
![]() ,-
,-![]() ,
,![]() ,-
,-![]() ,
,![]() ,-
,-![]() ,…
,…
(1) 写出第7,8,9项的三个数;
(2) 第2 018个数是什么?
(3) 如果这一列数无限排列下去,与 ____ 、____ 两数越来越接近?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com