
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() 的图象交于点A(﹣2,﹣5 ),C (5,n),交y轴于点B,交x轴于点D,那么不等式kx+b﹣
的图象交于点A(﹣2,﹣5 ),C (5,n),交y轴于点B,交x轴于点D,那么不等式kx+b﹣ ![]() >0的解集是 .
>0的解集是 . 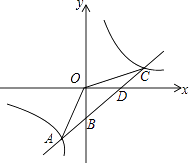
【答案】﹣2<x<0或x>5
【解析】解:∵反比例函数y= ![]() 的图象经过点A(﹣2,﹣5 ), ∴m=(﹣2)×(﹣5)=10,
的图象经过点A(﹣2,﹣5 ), ∴m=(﹣2)×(﹣5)=10,
∴反比例函数的表达式为y= ![]() ,
,
∵点C (5,n)在反比例函数的图象上,
∴n= ![]() =2,
=2,
∴C的坐标为C(5,2),
∵一次函数的图象经过点A,C,将这两个点的坐标代入y=kx+b,得![]() ,
,
解得 ![]() ,
,
∴一次函数的表达式为y=x﹣3,
根据图象法可得,当一次函数的图象在反比例函数的图象上边时,对应的自变量x的范围是:﹣2<x<0或x>5,
∴不等式x﹣3﹣ ![]() >0的解集是:﹣2<x<0或x>5.
>0的解集是:﹣2<x<0或x>5.
所以答案是:﹣2<x<0或x>5.
【考点精析】关于本题考查的确定一次函数的表达式,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽暑假期间参加社会实践活动,从某批发市场以批发价每个![]() 元的价格购进
元的价格购进![]() 个手机充电宝,然后每个加价
个手机充电宝,然后每个加价![]() 元到市场出售.
元到市场出售.
![]() 求售出
求售出![]() 个手机充电宝的总售价为多少元(结果用含
个手机充电宝的总售价为多少元(结果用含![]() ,
,![]() 的式子表示)?
的式子表示)?
![]() 由于开学临近,小丽在成功售出
由于开学临近,小丽在成功售出![]() 个充电宝后,决定将剩余充电宝按售价
个充电宝后,决定将剩余充电宝按售价![]() 折出售,并很快全部售完.
折出售,并很快全部售完.
①相比不采取降价销售,她将比实际销售多盈利多少元(结果用含![]() 、
、![]() 的式子表示)?
的式子表示)?
②若![]() ,小丽实际销售完这批充电宝的利润率为________(利润率
,小丽实际销售完这批充电宝的利润率为________(利润率![]() 利润
利润![]() 进价
进价![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3.5cm,则此光盘的直径是( )cm. 
A.7
B.![]()
C.![]()
D.14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】麒麟区第七中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,CD=13m,AD=12m.

(1)求出空地ABCD的面积?
(2)若每种植1平方米草皮需要300元,问总共需投入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)探究题:如图:
(1)△ABC为等边三角形,动点D在边CA上,动点P在边BC上,若这两点分别从C、B点同时出发,以相同的速度由C向A和由B向C运动,连接AP,BD交于点Q,两点运动过程中AP=BD成立吗?请证明你的结论;
(2)如果把原题中“动点D在边CA上,动点P边BC上,”改为“动点D,P在射线CA和射线BC上运动”,其他条
件不变,如图(2)所示,两点运动过程中∠BQP的大小保持不变.请你利用图(2)的情形,
求证:∠BQP=60°;
(3)如果把原题中“动点P在边BC上”改为“动点P在AB的延长线上运动,连接PD交BC于E”,其他条件不变,如图(3),则动点D,P在运动过程中,DE始终等于PE吗?写出证明过程.
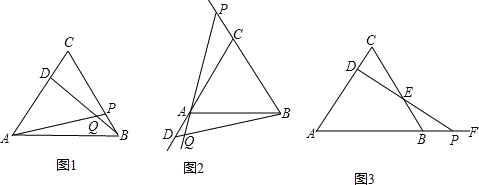
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |
(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2 , 在第四组内的两名选手记为:B1、B2 , 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平行四边形ABCD中,AB=5,AD=8,∠A=60°,点P为AD边上任意一点,连接PB,并将PB绕点P逆时针旋转90°得到线段PB′.
(1)当∠DP B′=20°时,∠ABP=____________;
(2)如图2,连结BB′,点P从A运动到D的过程中,求△PBB′面积的取值范围;
(3)若点B′恰好落在![]() ABCD边AD或BC所在的直线上时,直接写出AP的长.(结果保留根号,不必化简)
ABCD边AD或BC所在的直线上时,直接写出AP的长.(结果保留根号,不必化简)
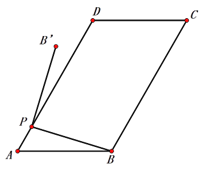
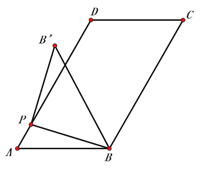
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
(1)求证:∠FMC=∠FCM;
(2)AD与MC垂直吗?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com