
����Ŀ����ͼ1����ƽ���ı���ABCD�У�AB��5��AD��8����A��60������PΪAD��������һ�㣬����PB������PB�Ƶ�P��ʱ����ת90���õ��߶�PB�䣮
��1������DP B�䣽20��ʱ����ABP��____________��
��2����ͼ2������BB������P��A�˶���D�Ĺ����У�����PBB�������ȡֵ��Χ��
��3������B��ǡ������![]() ABCD��AD��BC���ڵ�ֱ����ʱ��ֱ��д��AP�ij���������������ţ����ػ���
ABCD��AD��BC���ڵ�ֱ����ʱ��ֱ��д��AP�ij���������������ţ����ػ���
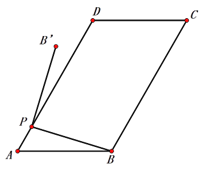
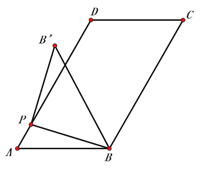
ͼ1 ͼ2
���𰸡�(1) 10���50��;(2) ![]()
![]() S��PBB��
S��PBB��![]()
![]() ;��3��AP=2.5��
;��3��AP=2.5��![]() .
.
��������������
��1������������ֵ�B����ƽ���ı���ABCD�ⲿ���ڲ��ֱ���з������ۣ�������B����ƽ���ı����ⲿʱ����ͼ1���������á�BPB��=90�㣬�����DPB��=20���ɵ���BPD=70�㣬�ɴ˿ɵ���APB=110�������A=60�����ɵõ���ABP=10�㣻����ͼ2������B����ƽ���ı����ڲ�ʱ������������DPB=��B��PB+��B��PD=90��+20��=110���������DPB=��A+��ABP���������ABP�Ķ�����
��2���������֪��PBB���ǵ���ֱ�����������ʵ���ֱ�DZ����ʱ���������С��������ֱ�DZ��ʱ����������������BP��ADʱ��PB��С����PB��BD�غ�ʱ��PB���������������з������㼴����������ȡֵ��Χ��
��3��������Ӧ��ͼ�Σ������֪�������з������.
��⣺
��1���������֪�����ڵ�B����ƽ���ı���ABCD�ⲿ���ڲ�����������ֱַ��������£�
������B����ƽ���ı���ABCD��ʱ��
�ߡ�DPB=��B��PB����B��PD=90�㩁20��=70�㣬
���ABP=��DPB����A=70�㩁60��=10�㣬

ͼ1
������B����ƽ���ı���ABCD��ʱ��
�ߡ�DPB=��B��PB+��B��PD=90��+20��=110�㣬
���ABP=��DPB����A=110�㩁60��=50�㣬
��������������DPQ=20��ʱ����APB=10����50����
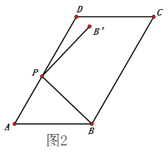
��2������ͼ3����Ȼ��BP��ADʱ��BP��С��
�ߡ�A=60�㣬AB=5��
��AP=2.5��
����ʱBP��С=![]() ��
��
����ʱS��PBB��=![]()
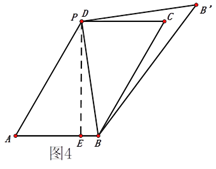
����ͼ4����Ȼ��P��D�غ�ʱ��BP���
��P����PE��AB�ڵ�E����ã�PE=![]() ��BE=1����BP=7.
��BE=1����BP=7.
����ʱS��PBB��=![]() ��
��
���ϣ�![]() S��PBB��
S��PBB��![]() .
.
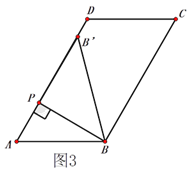
��3��AP=2.5��![]()
������B����AD��ʱ����ͼ3���ɣ�2����֪����ʱAP=2.5��
������B����ֱ��BC��ʱ����ͼ5����BE��AD�ڵ�E��
���AEB=��PEB=90�㣬
�ߡ�A=60�㣬AD��BC��
���ABE=30�㣬��CBE=120�㣬
��AE=![]() AB=2.5��BE=
AB=2.5��BE=![]() ����CBE=90�㣬
����CBE=90�㣬
�ߡ�BPB���ǵ���ֱ����������
���CBP=45�㣬
���PBE=45�㣬
��PE=BE=![]() ��
��
��AP=2.5+![]() ��
��
��������������B����ֱ��AD��ֱ��BC��ʱ��AP�ij�Ϊ2.5��2.5+![]() ��
��



 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�У�BD������һ���Խ��ߣ���A��C������AE��BD��CF��BD������ֱ�ΪE��F���ӳ�AE��CF�ֱ�CD��AB��M��N��
��1����֤���ı���CMAN��ƽ���ı��Σ�
��2����֪DE=2��FN=1����BN�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ���뷴��������y= ![]() ��ͼ���ڵ�A����2����5 ����C ��5��n������y���ڵ�B����x���ڵ�D����ô����ʽkx+b��
��ͼ���ڵ�A����2����5 ����C ��5��n������y���ڵ�B����x���ڵ�D����ô����ʽkx+b�� ![]() ��0�Ľ⼯�� ��
��0�Ľ⼯�� �� 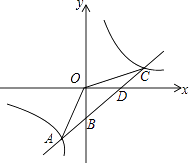
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������������y= ![]() ��ͼ����һ�κ���y=x+b��ͼ���ڵ�A��1��4������B����4��n����
��ͼ����һ�κ���y=x+b��ͼ���ڵ�A��1��4������B����4��n���� 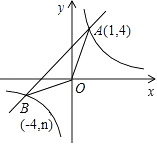
��1����һ�κ����ͷ����������Ľ���ʽ��
��2�����OAB�������
��3��ֱ��д��һ�κ���ֵ���ڷ���������ֵ���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ���������֣�������⣺���֪��![]() ������������������������ѭ��С�������
������������������������ѭ��С�������![]() ��С���������Dz�����ȫ��д����������С����
��С���������Dz�����ȫ��д����������С����![]() ����ʾ
����ʾ![]() ��С�����֣���ͬ��С���ı�ʾ��������ʵ�ϣ�С���ı�ʾ�������е����ģ���Ϊ
��С�����֣���ͬ��С���ı�ʾ��������ʵ�ϣ�С���ı�ʾ�������е����ģ���Ϊ![]() ������������1�����������ȥ���������֣������С�����֣������磺��22��7��3����2��
������������1�����������ȥ���������֣������С�����֣������磺��22��7��3����2��![]() ��3����
��3����![]() ����������Ϊ2��С������Ϊ
����������Ϊ2��С������Ϊ![]() ��2��
��2��
����
��1��![]() �������������� �������������� ����
�������������� �������������� ����
��2�����![]() ��С������Ϊa��
��С������Ϊa�� ![]() ����������Ϊb����a+b-
����������Ϊb����a+b-![]() ��ֵ��
��ֵ��
��3����֪��x��3+![]() ���������֣�y����С�����֣���ֱ��д��x��y��ֵ���෴����
���������֣�y����С�����֣���ֱ��д��x��y��ֵ���෴����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ȱ���ABC�ı߳�Ϊ4�� P��Q��R�ֱ�Ϊ��AB��BC��AC�ϵĶ��㣬��PR��QR����Сֵ�� _____.
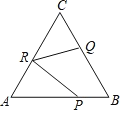
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����������y= ![]() ��x��0����ͼ������һ��A��m��4��������A��AB��x���ڵ�B������B����ƽ��2����λ���ȵõ���C������C��y���ƽ���߽�������������ͼ���ڵ�D��CD=
��x��0����ͼ������һ��A��m��4��������A��AB��x���ڵ�B������B����ƽ��2����λ���ȵõ���C������C��y���ƽ���߽�������������ͼ���ڵ�D��CD= ![]()
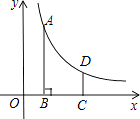
��1����D�ĺ�����Ϊ���ú�m��ʽ�ӱ�ʾ����
��2�����������Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������ABC�У�ADƽ�֡�BAC��AD��BC������ΪD��AN����ABC��ǡ�CAM��ƽ���ߣ�CE��AN������ΪE.
��1����֤���ı���ADCE�Ǿ��Σ�
��2������ABC����ʲô����ʱ���ı���ADCE�������Σ�����֤��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��֯��һ��G20֪ʶ����������ݻ�ͬѧ�ھ����еijɼ��Ƴɵ�ͳ��ͼ�����£���ϸ�Ķ�ͼ��������⣺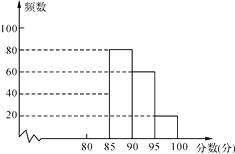
������ | Ƶ�� | Ƶ�� |
80��x��85 | a | 0.2 |
85��x��90 | 80 | b |
90��x��95 | 60 | c |
95��x��100 | 20 | 0.1 |
��1���������a��b��c����ֵ������ȫƵ���ֲ�ֱ��ͼ��
��2���ɼ�����λ�������ĸ������Σ�
��3������ȫ���ͬѧ�ɼ���ƽ���֣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com