
【题目】阅读下面的文字,解答问题:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部写出来,于是小明用
的小数部分我们不可能全部写出来,于是小明用![]() 来表示
来表示![]() 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<7<3,即2<
的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<7<3,即2<![]() <3,∴
<3,∴![]() 的整数部分为2,小数部分为
的整数部分为2,小数部分为![]() ﹣2.
﹣2.
请解答:
(1)![]() 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .
(2)如果![]() 的小数部分为a,
的小数部分为a, ![]() 的整数部分为b,求a+b-
的整数部分为b,求a+b-![]() 的值;
的值;
(3)已知:x是3+![]() 的整数部分,y是其小数部分,请直接写出x﹣y的值的相反数.
的整数部分,y是其小数部分,请直接写出x﹣y的值的相反数.
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】今年8月,我国空军八一飞行表演队赴俄罗斯国际军事技术论坛上进行飞行表演,其中一架飞机起飞后的高度变化如下表:

(1) 如果飞机每上升或下降1千米需消耗2升燃油,那么这架飞机在这4个动作表演过程中,一共消耗了多少升燃油?
(2) 如果飞机做特技表演时,有4个规定动作,起飞后高度变化如下:上升3.8千米,下降2.9千米,再上升1.6千米.若要使飞机最终比起飞点高出1千米,问第4个动作是上升还是下降,上升或下降多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】麒麟区第七中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,CD=13m,AD=12m.

(1)求出空地ABCD的面积?
(2)若每种植1平方米草皮需要300元,问总共需投入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |
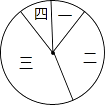
(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2 , 在第四组内的两名选手记为:B1、B2 , 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面的变形规律:
![]() ;
;![]() ;
;![]() ;….
;….
解答下面的问题:
(1)仿照上面的格式请写出![]() =_____;
=_____;
(2)若n为正整数,请你猜想![]() =_____;
=_____;
(3)基础应用:计算:![]() +
+![]() +
+![]()
![]() .
.
(4)拓展应用1:解方程:![]() +
+![]() +
+![]()
![]() =2016
=2016
(5)拓展应用2:计算:![]() +
+![]() +
+![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平行四边形ABCD中,AB=5,AD=8,∠A=60°,点P为AD边上任意一点,连接PB,并将PB绕点P逆时针旋转90°得到线段PB′.
(1)当∠DP B′=20°时,∠ABP=____________;
(2)如图2,连结BB′,点P从A运动到D的过程中,求△PBB′面积的取值范围;
(3)若点B′恰好落在![]() ABCD边AD或BC所在的直线上时,直接写出AP的长.(结果保留根号,不必化简)
ABCD边AD或BC所在的直线上时,直接写出AP的长.(结果保留根号,不必化简)
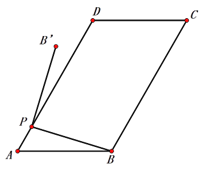
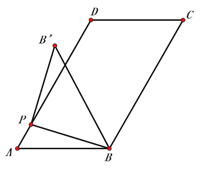
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,线段AC=6cm,线段BC=15cm,点M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长.
(2)如图2,∠BOE=2∠AOE,OF平分∠AOB,∠EOF=20°.求∠AOB.
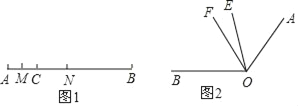
查看答案和解析>>
科目:初中数学 来源: 题型:
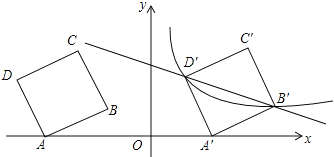
【题目】如图,在平面直角坐标系中,四边形ABCD为正方形,已知点A(![]() ,0)、D(
,0)、D(![]() ,3),点B、C在第二象限内.
,3),点B、C在第二象限内.
(1)点B的坐标 ;
(2)将正方形ABCD以每秒2个单位的速度沿x轴向右平移t秒,若存在某一时刻t,使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图像上,请求出此时t的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在y轴上的点P和反比例函数图像上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点P、Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中画出两条相交直线y=x和y=kx+b,交点为(x0 , y0),在x轴上表示出不与x0重合的x1 , 先在直线y=kx+b上确定点(x1 , y1),再在直线y=x上确定纵坐标为y1的点(x2 , y1),然后在x轴上确定对应的数x2 , …,依次类推到(xn , yn-1),我们来研究随着n的不断增加,xn的变化情况.如图1(注意:图在下页上),若k=2,b=—4,随着n的不断增加,xn逐渐(填“靠近”或“远离”)x0;如图2,若k= ![]() ,b=2,随着n的不断增加,xn逐渐(填“靠近”或“远离”)x0;若随着n的不断增加,xn逐渐靠近x0 , 则k的取值范围为 .
,b=2,随着n的不断增加,xn逐渐(填“靠近”或“远离”)x0;若随着n的不断增加,xn逐渐靠近x0 , 则k的取值范围为 . 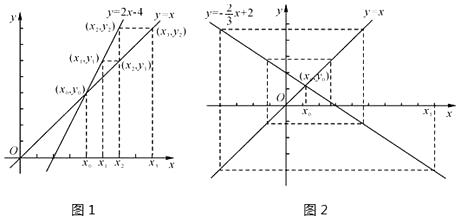
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com