
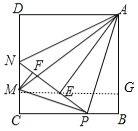
【题目】如图,在边长为2的正方形ABCD中,P是BC边上一动点(点P不与B、C重合),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA、NA,则以下结论:①△CMP∽△BPA;②四边形AMCB的面积最大值为2.5;③△ADN≌△AEN;④线段AM的最小值为2.5;⑤当P为BC中点时,AE为线段NP的中垂线.正确的有_____(只填序号)

【答案】①②③④
【解析】分析:①正确.只要证明∠CPM=∠PAB,∠C=∠B=90°,即可;
②正确,设PB=x,构建二次函数,利用二次函数性质解决问题即可;
③正确.根据HL即可证明;
④正确,作MG⊥AB于G,因为AM=![]() ,所以AG最小时AM最小,构建二次函数,求得AG的最小值为
,所以AG最小时AM最小,构建二次函数,求得AG的最小值为![]() ,AM的最小值为
,AM的最小值为![]() .
.
⑤错误,设ND=NE=y,在Rt△PCN中,利用勾股定理求出y即可解决问题.
详解:①由翻折可知,∠APE=∠APB,∠MPC=∠MPN,
∴∠APE+∠MPF=![]() ∠CPN+
∠CPN+![]() ∠BPE=90°,
∠BPE=90°,
∴∠CPM+∠APB=90°,∵∠APB+∠PAB=90°,
∴∠CPM=∠PAB,∵∠C=∠B=90°,
∴△CMP∽△BPA.故①正确;
②设PB=x,则CP=2-x,
∵△CMP∽△BPA,
∴![]() ,,
,,
∴CM=![]() x(2-x),
x(2-x),
∴S四边形AMCB=![]() [2+
[2+![]() x(2-x)]×2=-
x(2-x)]×2=-![]() x2+x+2=-
x2+x+2=-![]() (x-1)2+2.5,
(x-1)2+2.5,
∴x=1时,四边形AMCB面积最大值为2.5,故②正确;
③在Rt△ADN和Rt△AEN中,
![]() ,
,
∴△ADN≌△AEN.故③正确;
④作MG⊥AB于G,
∵AM=![]() ,
,
∴AG最小时AM最小,
∵AG=AB-BG=AB-CM=2-![]() x(2-x)=
x(2-x)=![]() (x-1)2+
(x-1)2+![]() ,
,
∴x=1时,AG最小值=![]() ,
,
∴AM的最小值=![]() ,故④正确.
,故④正确.
⑤当PB=PC=PE=1时,
由折叠知,ND=NE,
设ND=NE=y,
在Rt△PCN中,(y+1)2=(2-y)2+12解得y=![]()
∴NE=![]() ,
,
∴NE≠EP,故⑤错误,


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),与y轴相交于点C,动点M在线段OA和射线AC上运动。
(1)求直线AB的解析式;
(2)若△OMC的面积是△OAC的面积的![]() ,请直接写出此时点M的坐标 .
,请直接写出此时点M的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是甲、乙两人同一地点出发后,路程随时间变化的图象.

(1)两个变量中, 是自变量, 是因变量;
(2)甲的速度 乙的速度(填<、=、或>);
(3)路程为150km时,甲行驶了 小时,乙行驶了 小时.
(4)甲比乙先走了 小时;在9时, 走在前面。
查看答案和解析>>
科目:初中数学 来源: 题型:
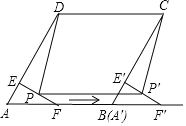
【题目】如图,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点,过点F作FE⊥AD,垂足为E,将△AEF沿点A到点B的方向平移,得到△A′E′F′.
(1)求EF的长;
(2)设P,P′分别是EF,E′F′的中点,当点A′与点B重合时,求证四边形PP′CD是平行四边形,并求出四边形PP′CD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区的三个景点A、B、C在同一线路上.甲、乙两名游客从景点A出发,甲步行到景点C;乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C,甲、乙两人同时到达景点C.甲、乙两人距景点A的路程y(米)与甲出发的时间x(分)之间的函数图象如图所示.
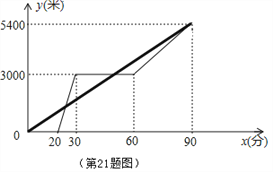
(1)乙步行的速度为_ __米/分.
(2)求乙乘景区观光车时y与x之间的函数关系式.
(3)甲出发多长时间与乙第一次相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程式应用题.
天河食品公司收购了200吨新鲜柿子,保质期15天,该公司有两种加工技术,一种是加工为普通柿饼,另一种是加工为特级霜降柿饼,也可以不需加工直接销售.相关信息见表:
品种 | 每天可加工数量(吨) | 每吨获利(元) |
新鲜柿子 | 不需加工 | 1000元 |
普通柿饼 | 16吨 | 5000元 |
特级霜降柿饼 | 8吨 | 8000元 |
由于生产条件的限制,两种加工方式不能同时进行,为此公司研制了两种可行方案:
方案1:尽可能多地生产为特级霜降柿饼,没来得及加工的新鲜柿子,在市场上直接销售;
方案2:先将部分新鲜柿子加工为特级霜降柿饼,再将剩余的新鲜柿子加工为普通柿饼,恰好15天完成.
请问:哪种方案获利更多?获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
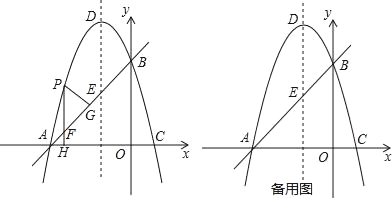
【题目】如图,在平面直角坐标系xoy中,直线y=x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线y=﹣x2+bx+c交x轴于另一点C,点D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)点P是直线AB上方的抛物线上一点,(不与点A、B重合),过点P作x轴的垂线交x轴于点H,交直线AB于点F,作PG⊥AB于点G.求出△PFG的周长最大值;
(3)在抛物线y=﹣x2+bx+c上是否存在除点D以外的点M,使得△ABM与△ABD的面积相等?若存在,请求出此时点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知□ABCD的面积为100,P为边CD上的任一点,E,F分别为线段AP,BP的中点,则图中阴影部分的总面积为( )

A. 30B. 25C. 22.5D. 20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com