
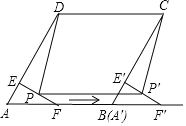
【题目】如图,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点,过点F作FE⊥AD,垂足为E,将△AEF沿点A到点B的方向平移,得到△A′E′F′.
(1)求EF的长;
(2)设P,P′分别是EF,E′F′的中点,当点A′与点B重合时,求证四边形PP′CD是平行四边形,并求出四边形PP′CD的面积.
【答案】(1)2![]() ;(2)28
;(2)28![]() .
.
【解析】
(1)首先求出AF的长度,再在直角三角形AEF中求出EF的长度;
(2)连接BD,DF,DF交PP′于H.首先证明四边形PP′CD是平行四边形,再证明DF⊥PP′,求出DH的长,最后根据面积公式求出答案.
(1)∵四边形ABCD是菱形,
∴AD=AB=8,
∵F是AB的中点,
∴AF=![]() AB=
AB=![]() ×8=4,
×8=4,
∵点F作FE⊥AD,∠A=60°,
∴∠AFE=30°,
∴AE=![]() ,
,
∴EF=2![]() ;
;
(2)如图,连接BD,DF,DF交PP′于H.

由题意PP′=AA′=AB=CD,PP′∥AA′∥CD,
∴四边形PP′CD是平行四边形,
∵四边形ABCD是菱形,∠A=60°,
∴△ABD是等边三角形,
∵AF=FB,
∴DF⊥AB,DF⊥PP′,
在Rt△AEF中,∵∠AEF=90°,∠A=60°,AF=4,
∴AE=2,EF=2![]() ,
,
∴PE=PF=![]() ,
,
在Rt△PHF中,∵∠FPH=30°,PF=![]() ,
,
∴HF=![]() PF=
PF=![]() ,
,
∵DF=![]() =4
=4![]() ,
,
∴DH=4![]() ﹣
﹣![]() =
=![]() ,
,
∴平行四边形PP′CD的面积=![]() ×8=28
×8=28![]() .
.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线y=kx+b交x轴于点A,交y轴于点B,直线y=2x﹣4交x轴于点D,与直线AB相交于点C(3,2).
(1)根据图象,写出关于x的不等式2x﹣4>x+b的解集;
(2)若点A的坐标为(5,0),求直线AB的解析式;
(3)在(2)的条件下,求四边形BODC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
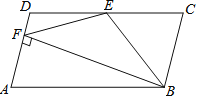
【题目】如图,在平行四边形ABCD中,AB=2AD,BE平分∠ABC交CD于点E,作BF⊥AD,垂足为F,连接EF,小明得到三个结论:①∠FBC=90°;②ED=EB;③S△EBF=S△EDF+S△EBC;则三个结论中一定成立的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角项点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
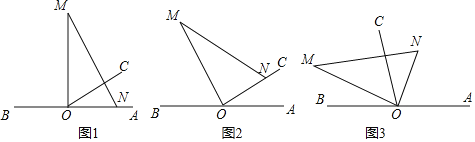
(1)将图1中的三角板绕点O以每秒5°的速度沿逆时针方向旋转一周.如图2,经过t秒后,ON落在OC边上,则t= 秒(直接写结果).
(2)在(1)的条件下,若三角板继续转动,同时射线OC也绕O点以每秒10°的速度沿逆时针方向旋转一周,当OC转动9秒时,求∠MOC的度数.
(3)在(2)的条件下,它们继续运动多少秒时,∠MOC=35°?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示数1,现将点A沿数轴做如下移动:第一次将点A向左移动3个单位长度到达点![]() ,第2次将点
,第2次将点![]() 向右平移6个单位长度到达点
向右平移6个单位长度到达点![]() ,第3次将点
,第3次将点![]() 向左移动9个单位长度到达点
向左移动9个单位长度到达点![]() …,按照这种规律移动下去,则第2017次移动到点
…,按照这种规律移动下去,则第2017次移动到点![]() 时,
时,![]() 在数轴上对应的实数是_______.
在数轴上对应的实数是_______.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种西装和领带,西装每套定价200元,领带每条定价40元.国庆节期间商场决定开展促销活动,活动期间向客户提供两种优惠方案:
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x![]() .
.
(1)若该客户按方案一购买,需付款多少元(用含x的式子表示)?若该客户按方案二购买,需付款多少元(用含x的式子表示)?
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算;
,通过计算说明此时按哪种方案购买较为合算;
(3)当![]() 时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,P是BC边上一动点(点P不与B、C重合),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA、NA,则以下结论:①△CMP∽△BPA;②四边形AMCB的面积最大值为2.5;③△ADN≌△AEN;④线段AM的最小值为2.5;⑤当P为BC中点时,AE为线段NP的中垂线.正确的有_____(只填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂计划平均每天生产200辆,但是由于种种原因,实际每天生产量与计划量相比有出入。表是某周的生产情况(超产记为正,减产记为负):

(1)根据记录的数据可知该厂星期三生产自行车多少辆?
(2)产量最多的一天比产量最少的一天多生产自行车多少辆?
(3)根据记录的数据可知该厂本周实际共生产自行车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为任意三角形,以AB、AC为边分别向外做等边△ABD和等边△ACE,连接CD、BE并相交于点P.求证:
(1)CD=BE;
(2)∠BPC=120°.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com