【题目】如图，在数轴上，点A表示数1,现将点A沿数轴做如下移动：第一次将点A向左移动3个单位长度到达点
，第2次将点向右平移6个单位长度到达点
，第3次将点向左移动9个单位长度到达点
…，按照这种规律移动下去，则第2017次移动到点
时，在数轴上对应的实数是_______.
科目：初中数学 来源： 题型：
【题目】如图的⊙O中，AB为直径，OC⊥AB，弦CD与OB交于点F，过点D、A分别作⊙O的切线交于点G，并与AB延长线交于点E．
（1）求证：∠1=∠2．
（2）已知：OF：OB=1：3，⊙O的半径为3，求AG的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是甲、乙两人同一地点出发后，路程随时间变化的图象．
（1）两个变量中， 是自变量， 是因变量；
（2）甲的速度 乙的速度（填<、=、或>）；
（3）路程为150km时，甲行驶了 小时，乙行驶了 小时．
（4）甲比乙先走了 小时；在9时， 走在前面。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知直线
与双曲线y＝
交于A、B两点，点B的坐标为(-4，-2)，C为第一象限内双曲线y＝
上一点，且点C在直线
的上方．
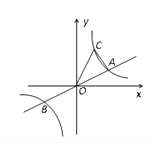
(1)求双曲线的函数解析式；
(2)若△AOC的面积为6，求点C的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
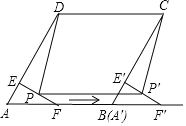
【题目】如图，在菱形ABCD中，∠A＝60°，AD＝8，F是AB的中点，过点F作FE⊥AD，垂足为E，将△AEF沿点A到点B的方向平移，得到△A′E′F′．
（1）求EF的长；
（2）设P，P′分别是EF，E′F′的中点，当点A′与点B重合时，求证四边形PP′CD是平行四边形，并求出四边形PP′CD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某景区的三个景点A、B、C在同一线路上．甲、乙两名游客从景点A出发，甲步行到景点C;乙乘景区观光车先到景点B，在B处停留一段时间后，再步行到景点C，甲、乙两人同时到达景点C．甲、乙两人距景点A的路程y(米)与甲出发的时间x(分)之间的函数图象如图所示．
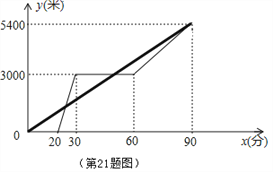
（1）乙步行的速度为_ __米/分．
（2）求乙乘景区观光车时y与x之间的函数关系式．
（3）甲出发多长时间与乙第一次相遇?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】列方程式应用题．
天河食品公司收购了200吨新鲜柿子，保质期15天，该公司有两种加工技术，一种是加工为普通柿饼，另一种是加工为特级霜降柿饼，也可以不需加工直接销售．相关信息见表：
品种 | 每天可加工数量（吨） | 每吨获利（元） |
新鲜柿子 | 不需加工 | 1000元 |
普通柿饼 | 16吨 | 5000元 |
特级霜降柿饼 | 8吨 | 8000元 |
由于生产条件的限制，两种加工方式不能同时进行，为此公司研制了两种可行方案：
方案1：尽可能多地生产为特级霜降柿饼，没来得及加工的新鲜柿子，在市场上直接销售；
方案2：先将部分新鲜柿子加工为特级霜降柿饼，再将剩余的新鲜柿子加工为普通柿饼，恰好15天完成．
请问：哪种方案获利更多？获利多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在等腰直角△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．
（1）求证：△ADC≌△CEB；
（2）求证：AD+BE=DE；
（3）当直线MN绕点C旋转到图2的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以说明．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
