
【题目】如图,已知直线![]() 与双曲线y=
与双曲线y=![]() 交于A、B两点,点B的坐标为(-4,-2),C为第一象限内双曲线y=
交于A、B两点,点B的坐标为(-4,-2),C为第一象限内双曲线y=![]() 上一点,且点C在直线
上一点,且点C在直线![]() 的上方.
的上方.
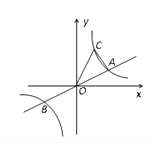
(1)求双曲线的函数解析式;
(2)若△AOC的面积为6,求点C的坐标.
【答案】(1) ![]() ;(2)(2,4)
;(2)(2,4)
【解析】试题分析:(1)利用待定系数法即可解决.
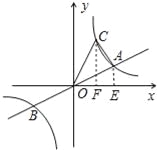
(2)过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,根据![]() =6,列出方程即可解决.
=6,列出方程即可解决.
试题解析:(1)∵点B(﹣4,﹣2)在双曲线y=![]() 上,
上,
∴![]() =﹣2,
=﹣2,
∴k=8,
∴双曲线的函数解析式为y=![]() .
.
(2)过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,
∵正比例函数与反比例函数的交点A、B关于原点对称,
∴A(4,2),∴OE=4,AE=2,
设点C的坐标为(a, ![]() ),则OF=a,CF=
),则OF=a,CF=![]() ,
,
则![]() ,
,
=![]() ×
×![]() +
+![]() (2+
(2+![]() )(4﹣a)﹣
)(4﹣a)﹣![]() ×4×2
×4×2
=![]() ,
,
∵△AOC的面积为6,
∴![]() =6,
=6,
整理得a2+6a﹣16=0,
解得a=2或﹣8(舍弃),
∴点C的坐标为(2,4).


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】下列命题中错误的有( )个
(1)等腰三角形的两个底角相等
(2)对角线相等且互相垂直的四边形是正方形
(3)对角线相等的四边形为矩形
(4)圆的切线垂直于半径
(5)平分弦的直径垂直于弦
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.
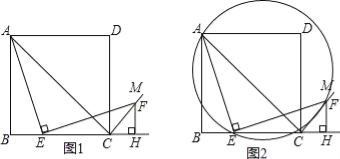
(1)试判断BE与FH的数量关系,并说明理由;
(2)求证:∠ACF=90°;
(3)连接AF,过A、E、F三点作圆,如图2,若EC=4,∠CEF=15°,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列条件可列出一元一次方程的是( )
A. a与1的和的3倍
B. 甲数的2倍与乙数的3倍的和
C. a与b的差的20%
D. 一个数的3倍是5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级在开展“学会感恩“的活动月中,对九年级(2)班40人一周内(周一至周五)零花钱的使用情况进行调查,结果如下表:
人数 | 5 | 15 | 13 | 7 |
使用零花钱(单位:元) | 15 | 20 | 30 | 35 |
那么学生使用零花钱的中位数和众数分别是( )
A. 15和35 B. 20和20 C. 15和20 D. 20和25
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com