
【题目】如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.
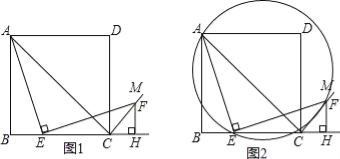
(1)试判断BE与FH的数量关系,并说明理由;
(2)求证:∠ACF=90°;
(3)连接AF,过A、E、F三点作圆,如图2,若EC=4,∠CEF=15°,求![]() 的长.
的长.
【答案】(1)BE=FH;(2)证明见解析(3)2π
【解析】
试题分析:(1)利用ABE≌△EHF求证BE=FH,
(2)由BE=FH,AB=EH,推出CH=FH,得到∠HCF=45°,由四边形ABCD是正方形,所以∠ACB=45°,得出∠ACF=90°,
(3)作CP⊥EF于P,利用相似三角形△CPE∽△FHE,求出EF,利用公式求出![]() 的长.
的长.
试题解析:(1)BE=FH.
证明:∵∠AEF=90°,∠ABC=90°,
∴∠HEF+∠AEB=90°,∠BAE+∠AEB=90°,
∴∠HEF=∠BAE,
在△ABE和△EHF中,
 ,
,
∴△ABE≌△EHF(AAS)
∴BE=FH.
(2)由(1)得BE=FH,AB=EH,
∵BC=AB,
∴BE=CH,
∴CH=FH,
∴∠HCF=45°,
∵四边形ABCD是正方形,
∴∠ACB=45°,
∴∠ACF=180°﹣∠HCF﹣∠ACB=90°.
(3)由(2)知∠HCF=45°,∴CF=![]() FH.
FH.
∠CME=∠HCF﹣∠CEF=45°﹣15°=30°.
如图2,过点C作CP⊥EF于P,则CP=![]() CF=
CF=![]() FH.
FH.

∵∠CEP=∠FEH,∠CPE=∠FHE=90°,
∴△CPE∽△FHE.
∴![]() ,即
,即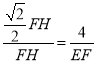 ,
,
∴EF=4![]() .
.
∵△AEF为等腰直角三角形,∴AF=8.
取AF中点O,连接OE,则OE=OA=4,∠AOE=90°,
∴![]() 的弧长为:
的弧长为:![]() =2π.
=2π.


科目:初中数学 来源: 题型:
【题目】植树节期间,某单位欲购进A、B两种树苗,若购进A种树苗3棵,B种树苗5棵,需2100元,若购进A种树苗4棵,B种树苗10棵,需3800元.
(1)求购进A、B两种树苗的单价;
(2)若该单位准备用不多于8000元的钱购进这两种树苗共30棵,求A种树苗至少需购进多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一件商品按成本价提高40%后标价,再打8折(标价的80%)销售,售价为240元,设这件商品的成本价为x元,根据题意,下面所列的方程正确的是( )
A. 40%x·80%=240
B. (1+40%)x·80%=240
C. 240×40%×80%=x
D. 40%x=240×80%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与双曲线y=
与双曲线y=![]() 交于A、B两点,点B的坐标为(-4,-2),C为第一象限内双曲线y=
交于A、B两点,点B的坐标为(-4,-2),C为第一象限内双曲线y=![]() 上一点,且点C在直线
上一点,且点C在直线![]() 的上方.
的上方.
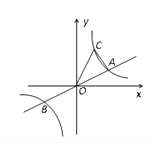
(1)求双曲线的函数解析式;
(2)若△AOC的面积为6,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种药品说明书上标明保存温度是(20±3)0C,则该药品在( )范围内保存最合适.
A. 170C~200C B. 200C ~230C C. 170C ~230C D. 170C ~240C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列等式变形不正确的是( )
A. 由x=y,得到x+2=y+2
B. 由2a﹣3=b﹣3,得到2a=b
C. 由m=n,得到2am=2an
D. 由am=an,得到m=n
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com