
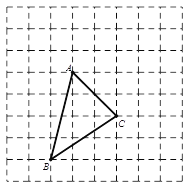
【题目】如图,在由边长为1的小正方形组成的网格图中有一个格点三角形ABC.(注:顶点均在网格线交点处的三角形称为格点三角形)
(1)请直接写出sin∠ABC的值: ;
(2)请在图中画格点三角形DEF,使得△DEF∽△ABC,且相似比为2∶1;
(3)请在图中确定格点M,使得△BCM的面积为6.如果符合题意的格点M不止一个,请分别用M1、M2、M3…表示.
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
轴交于A(-3,0),B(1,0)两点,与y轴交于点C.

(1)求这个二次函数的解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
(3)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于![]() 轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
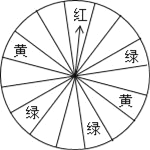
【题目】“六一”儿童节期间,某商厦为了吸引顾客,设立了一个可以自由转动的转盘(转盘被平均分成16份),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准哪个区域,顾客就可以获得相应的奖品.
颜色 | 奖品 |
红色 | 玩具熊 |
黄色 | 童话书 |
绿色 | 彩笔 |
小明和妈妈购买了125元的商品,请你分析计算:
(1)小明获得奖品的概率是多少?
(2)小明获得童话书的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与理解:
如图,一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行.若我们规定:在如图网格中,向上(或向右)爬行记为“+”,向下(或向左)爬行记为“﹣”,并且第一个数表示左右方向,第二个数表示上下方向.
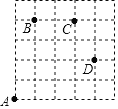
例如:从A到B记为:A→B(+1,+4),从D到C记为:D→C(﹣1,+2).
思考与应用:
(1)图中B→C( , )C→D( , )
(2)若甲虫从A到P的行走路线依次为:(+3,+2)→(+1,+3)→(+1,﹣2),请在图中标出P的位置.
(3)若甲虫的行走路线为A→(+1,+4)→(+2,0)→(+1,﹣2)→(﹣4,﹣2),请计算该甲虫走过的总路程S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,点F 是CD延长线上的一点,且AD平分∠BDF,AE⊥CD于点E.

⑴ 求证:AB=AC.
⑵ 若BD=11,DE=2,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 分别在边
分别在边![]() ,
,![]() ,
,![]() 上,且
上,且![]() ,
,![]() .下列四个判断中,不正确的是( )
.下列四个判断中,不正确的是( )

A. 四边形![]() 是平行四边形
是平行四边形
B. 如果![]() ,那么四边形
,那么四边形![]() 是矩形
是矩形
C. 如果![]() 平分平分∠BAC,那么四边形 AEDF 是菱形
平分平分∠BAC,那么四边形 AEDF 是菱形
D. 如果AD⊥BC 且 AB=AC,那么四边形 AEDF 是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,△ABC中,∠C=90°,AB的垂直平分线交AC于点D,连接BD. 若AC=2,BC=1,则△BCD的周长为___________________.
(2)O为正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.
①在图2中求作△EDF.(要求:尺规作图,不写作法,保留作图痕迹)
②在图3中补全图形,求∠EOF的度数.
③若![]() ,则
,则![]() =_______________.
=_______________.

图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB=![]() (
(![]() 为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足CQ=2AQ,CP=2BP.
为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足CQ=2AQ,CP=2BP.
(1)如图,当点C恰好在线段AB中点时,则PQ=_______(用含![]() 的代数式表示);
的代数式表示);
(2)若点C为直线AB上任一点,则PQ长度是否为常数?若是,请求出这个常数;若不是,请说明理由;
(3)若点C在点A左侧,同时点P在线段AB上(不与端点重合),请判断2AP+CQ-2PQ与1的大小关系,并说明理由。
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com