
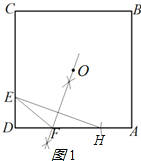
【题目】(1)如图1,△ABC中,∠C=90°,AB的垂直平分线交AC于点D,连接BD. 若AC=2,BC=1,则△BCD的周长为___________________.
(2)O为正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.
①在图2中求作△EDF.(要求:尺规作图,不写作法,保留作图痕迹)
②在图3中补全图形,求∠EOF的度数.
③若![]() ,则
,则![]() =_______________.
=_______________.

图1 图2 图3
【答案】(1)3;(2)①作图见解析;②45°;③![]() .
.
【解析】试题分析:(1)由线段垂直平分线的性质得出BD=AD,得出△BCD的周长=BC+CD+BD=BC+AC,即可得出结果;
(2)①在AD上截取AH=DE,再作EG的垂直平分线,交AD于F,△EDF即为所求;
②连接OA、OD、OH,由正方形的性质得出∠1=∠2=45°,由SAS证明△ODE≌△OAH,得出∠DOE=∠AOH,OE=OH,得出∠EOH=90°,证出EF=HF,由SSS证明△EOF≌△HOF,得出∠EOF=∠HOF=45°即可;
③作OG⊥CD于G,OK⊥AD于K,设AF=8t,则CE=9t,设OG=m,由正方形的性质得出GE=CE-CG=9t-m,DE=2CG-CE=2m-9t,FK=AF-KA=8t-m,DF=2DK-AF=2m-8t,由HL证明Rt△EOG≌Rt△HOK,得出GE=KH,因此EF=GE+FK=17t-2m,由勾股定理得出方程,解方程求出m=6t,得出OG=OK=6t,GE=9t-m=9t-6t=3t,FK=8t-m=2t,由勾股定理即可得出结果.
试题解析:(1)∵AB的垂直平分线交AC于点D,
∴BD=AD,
∴△BCD的周长=BC+CD+BD=BC+AC=1+2=3,
故答案为:3;
(2)①如图1所示:△EDF即为所求;
②如图2所示:
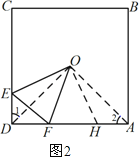
AH=DE,连接OA、OD、OH,
∵点O为正方形ABCD的中心,
∴OA=OD,∠AOD=90°,∠1=∠2=45°,
在△ODE和△OAH中,
 ,
,
∴△ODE≌△OAH(SAS),
∴∠DOE=∠AOH,OE=OH,
∴∠EOH=90°,
∵△EDF的周长等于AD的长,
∴EF=HF,
在△EOF和△HOF中,
 ,
,
∴△EOF≌△HOF(SSS),
∴∠EOF=∠HOF=45°;
③作OG⊥CD于G,OK⊥AD于K,如图3所示:

设AF=8t,则CE=9t,设OG=m,
∵O为正方形ABCD的中心,
∴四边形OGDK为正方形,CG=DG=DK=KA=![]() AB=OG,
AB=OG,
∴GE=CE﹣CG=9t﹣m,DE=2CG﹣CE=2m﹣9t,FK=AF﹣KA=8t﹣m,DF=2DK﹣AF=2m﹣8t,
由(2)②知△EOF≌△HOF,
∴OE=OH,EF=FH,
在Rt△EOG和Rt△HOK中,
![]() ,
,
∴Rt△EOG≌Rt△HOK(HL),
∴GE=KH,
∴EF=GE+FK=9t﹣m+8t﹣m=17t﹣2m,
由勾股定理得:DE2+DF2=EF2,
∴(2m﹣9t)2+(2m﹣8t)2=(17t﹣2m)2,
整理得:(m+6t)(m﹣6t)=0,
∴m=6t,
∴OG=OK=6t,GE=9t﹣m=9t﹣6t=3t,FK=8t﹣m=2t,
∴ =
=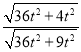 =
=![]() =
=![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
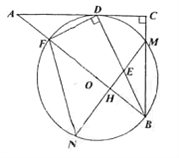
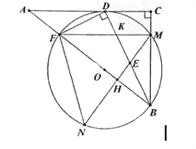
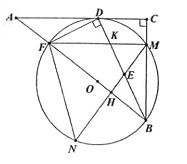
【题目】如图,在Rt△ABC中,∠C=90°,D为AC上一点,连接BD,DF⊥BD交AB于点F,△BDF的外接圆⊙O与边BC相较于点M,与AC相切于点D。过点M作AB的垂线交BD于点E,交⊙O于点N,交AB于点H,连接FN.
(1)求证:BD平分∠ABC;
(2)连接FM与BD相交于点K,求证:MK=ME;
(3)若AF=1,tan∠N=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
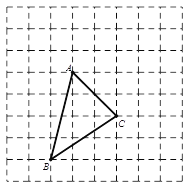
【题目】如图,在由边长为1的小正方形组成的网格图中有一个格点三角形ABC.(注:顶点均在网格线交点处的三角形称为格点三角形)
(1)请直接写出sin∠ABC的值: ;
(2)请在图中画格点三角形DEF,使得△DEF∽△ABC,且相似比为2∶1;
(3)请在图中确定格点M,使得△BCM的面积为6.如果符合题意的格点M不止一个,请分别用M1、M2、M3…表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校为了创建“书香校园”,购买了一批图书,其中科普类图书平均每本的 价格比文学类图书平均每本的价格多4元,已知学校用16000元购买的科普类图书的本数与用12000元购买的文学类图书的本数相等.求学校购买的科普类图书和文学类图书平均每本的价格各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,开口向上的抛物线与![]() 轴交于
轴交于![]() 两点,
两点, ![]() 为抛物线的顶点,
为抛物线的顶点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() . 若
. 若![]() 的长分别是方程
的长分别是方程![]() 的两根,且
的两根,且![]()
(1)求抛物线对应的二次函数解析式和点![]() 的坐标。
的坐标。
(2)若点M为x轴正半轴上一个动点,N为线段AC上的一个动点,连接MN、CM,是否存在这样的点M,使△AMN为直角三角形和△CMN为等腰三角形同时成立,如果存在,请求出所有符合条件的点M的坐标,如果不存在,请说明理由。
(3如图2,过点![]() 任作直线
任作直线![]() 交线段
交线段![]() 于点
于点![]() 求
求![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,请直接写出
,请直接写出![]() 的最大值.
的最大值.

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个直角三角形的直角顶点重合,∠AOC=40°,求∠BOD 的度数.
结合图形,完成填空:
解法 1:
因为![]() ,
,![]()
所以![]()
![]()
因为![]()
![]()
所以![]()
![]()
![]()
所以![]()
![]()
解法2:
因为![]()
![]() ,
,![]()
![]() ,①
,①
所以![]() .②
.②
因为![]()
所以![]()
![]()
在上面①到②的推导过程中,理由依据是: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个“磁悬浮”的轨道架上做钢球碰撞实验,如图 1 所示,轨道长为 180![]() ,轨道架上有三个大小、质量完全相同的钢球
,轨道架上有三个大小、质量完全相同的钢球![]() 、
、![]() 、
、![]() ,轨道左右各有一个钢制挡板
,轨道左右各有一个钢制挡板 ![]() 和
和 ![]() ,其中
,其中![]() 到左挡板的距离为 30
到左挡板的距离为 30![]() ,
,![]() 到右挡板的距离为 60
到右挡板的距离为 60![]() ,
,![]() 、
、![]() 两球相距40
两球相距40![]() .现以轨道所在直线为数轴,假定
.现以轨道所在直线为数轴,假定![]() 球在原点,
球在原点,![]() 球代表的数为 40,如图 2 所示,解答下列问题:
球代表的数为 40,如图 2 所示,解答下列问题:

(1)在数轴上,找出 ![]() 球及右挡板
球及右挡板 ![]() 所代表的数,并填在图中括号内.
所代表的数,并填在图中括号内.

(2)碰撞实验中(钢球大小、相撞时间不记),钢球的运动都是匀速,当一钢球以一速度撞向另一静止钢球时,这个钢球停留在被撞钢球的位置,被撞钢球则以同样的速度向前运动,钢球撞到左右挡板则以相同的速度反向运动.
①现 ![]() 球以每秒 10
球以每秒 10![]() 的速度向右匀速运动,则
的速度向右匀速运动,则 ![]() 球第二次到达
球第二次到达![]() 球所在位置时用了 秒;经过 63 秒时,
球所在位置时用了 秒;经过 63 秒时,![]() 、
、![]() 、
、![]() 三球在数轴上所对应的数分别是 、 、 ;
三球在数轴上所对应的数分别是 、 、 ;
②如果![]() 、
、![]() 两球同时开始运动,
两球同时开始运动,![]() 球向左运动,
球向左运动,![]() 球向右运动,
球向右运动,![]() 球速度是每秒 8
球速度是每秒 8![]() ,
,![]() 球速度是每秒 12
球速度是每秒 12![]() ,问:经过多少时间
,问:经过多少时间 ![]() 、
、![]() 两球相撞?相撞时在数轴上所对应的数是多少?
两球相撞?相撞时在数轴上所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示.

(1)补充完成下面的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 | 3.41 | 90% | 20% | |
乙组 | 7.5 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知将一副三角板(直角三角板![]() 和直角三角板
和直角三角板![]() )的两个顶点重合于点
)的两个顶点重合于点![]() .
.

(1)如图1,将直角三角板![]() 绕点
绕点![]() 逆时针方向转动,当
逆时针方向转动,当![]() 恰好平分
恰好平分![]() 时,
时,![]() 的度数是 _.
的度数是 _.
(2)如图2,当三角板![]() 摆放在
摆放在![]() 内部时,作射线
内部时,作射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() ,如果三角板
,如果三角板![]() 在
在![]() 内绕点
内绕点![]() 任意转动,
任意转动,![]() 的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
(3)当三角板![]() 绕点
绕点![]() 继续转动到如图3所示的位置时,作射线
继续转动到如图3所示的位置时,作射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() ,请你求出此时钝角
,请你求出此时钝角![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com