
ЁОЬтФПЁПдквЛИіЁАДХаќИЁЁБЕФЙьЕРМмЩЯзіИжЧђХізВЪЕбщЃЌШчЭМ 1 ЫљЪОЃЌЙьЕРГЄЮЊ 180![]() ЃЌЙьЕРМмЩЯгаШ§ИіДѓаЁЁЂжЪСПЭъШЋЯрЭЌЕФИжЧђ
ЃЌЙьЕРМмЩЯгаШ§ИіДѓаЁЁЂжЪСПЭъШЋЯрЭЌЕФИжЧђ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌЙьЕРзѓгвИїгавЛИіИжжЦЕВАх
ЃЌЙьЕРзѓгвИїгавЛИіИжжЦЕВАх ![]() КЭ
КЭ ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЕНзѓЕВАхЕФОрРыЮЊ 30
ЕНзѓЕВАхЕФОрРыЮЊ 30![]() ЃЌ
ЃЌ![]() ЕНгвЕВАхЕФОрРыЮЊ 60
ЕНгвЕВАхЕФОрРыЮЊ 60![]() ЃЌ
ЃЌ![]() ЁЂ
ЁЂ![]() СНЧђЯрОр40
СНЧђЯрОр40![]() ЃЎЯжвдЙьЕРЫљдкжБЯпЮЊЪ§жсЃЌМйЖЈ
ЃЎЯжвдЙьЕРЫљдкжБЯпЮЊЪ§жсЃЌМйЖЈ![]() ЧђдкдЕуЃЌ
ЧђдкдЕуЃЌ![]() ЧђДњБэЕФЪ§ЮЊ 40ЃЌШчЭМ 2 ЫљЪОЃЌНтД№ЯТСаЮЪЬтЃК
ЧђДњБэЕФЪ§ЮЊ 40ЃЌШчЭМ 2 ЫљЪОЃЌНтД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉдкЪ§жсЩЯЃЌевГі ![]() ЧђМАгвЕВАх
ЧђМАгвЕВАх ![]() ЫљДњБэЕФЪ§ЃЌВЂЬюдкЭМжаРЈКХФк.
ЫљДњБэЕФЪ§ЃЌВЂЬюдкЭМжаРЈКХФк.

ЃЈ2ЃЉХізВЪЕбщжаЃЈИжЧђДѓаЁЁЂЯрзВЪБМфВЛМЧЃЉЃЌИжЧђЕФдЫЖЏЖМЪЧдШЫйЃЌЕБвЛИжЧђвдвЛЫйЖШзВЯђСэвЛОВжЙИжЧђЪБЃЌетИіИжЧђЭЃСєдкБЛзВИжЧђЕФЮЛжУЃЌБЛзВИжЧђдђвдЭЌбљЕФЫйЖШЯђЧАдЫЖЏЃЌИжЧђзВЕНзѓгвЕВАхдђвдЯрЭЌЕФЫйЖШЗДЯђдЫЖЏ.
ЂйЯж ![]() ЧђвдУПУы 10
ЧђвдУПУы 10![]() ЕФЫйЖШЯђгвдШЫйдЫЖЏЃЌдђ
ЕФЫйЖШЯђгвдШЫйдЫЖЏЃЌдђ ![]() ЧђЕкЖўДЮЕНДя
ЧђЕкЖўДЮЕНДя![]() ЧђЫљдкЮЛжУЪБгУСЫ УыЃЛОЙ§ 63 УыЪБЃЌ
ЧђЫљдкЮЛжУЪБгУСЫ УыЃЛОЙ§ 63 УыЪБЃЌ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§ЧђдкЪ§жсЩЯЫљЖдгІЕФЪ§ЗжБ№ЪЧ ЁЂ ЁЂ ЃЛ
Ш§ЧђдкЪ§жсЩЯЫљЖдгІЕФЪ§ЗжБ№ЪЧ ЁЂ ЁЂ ЃЛ
ЂкШчЙћ![]() ЁЂ
ЁЂ![]() СНЧђЭЌЪБПЊЪМдЫЖЏЃЌ
СНЧђЭЌЪБПЊЪМдЫЖЏЃЌ![]() ЧђЯђзѓдЫЖЏЃЌ
ЧђЯђзѓдЫЖЏЃЌ![]() ЧђЯђгвдЫЖЏЃЌ
ЧђЯђгвдЫЖЏЃЌ![]() ЧђЫйЖШЪЧУПУы 8
ЧђЫйЖШЪЧУПУы 8![]() ЃЌ
ЃЌ![]() ЧђЫйЖШЪЧУПУы 12
ЧђЫйЖШЪЧУПУы 12![]() ЃЌЮЪЃКОЙ§ЖрЩйЪБМф
ЃЌЮЪЃКОЙ§ЖрЩйЪБМф ![]() ЁЂ
ЁЂ![]() СНЧђЯрзВЃПЯрзВЪБдкЪ§жсЩЯЫљЖдгІЕФЪ§ЪЧЖрЩйЃП
СНЧђЯрзВЃПЯрзВЪБдкЪ§жсЩЯЫљЖдгІЕФЪ§ЪЧЖрЩйЃП
ЁОД№АИЁПЃЈ1ЃЉ![]() ЧђДњБэЕФЪ§ЪЧ-50ЃЌ
ЧђДњБэЕФЪ§ЪЧ-50ЃЌ![]() ЧђДњБэЕФЪ§ЪЧ100ЃЛЃЈ2ЃЉЂй40ЃЛ-50ЃЛ40ЃЌ-70ЃЛЂкОЙ§16УыСНЧђЯрзВЃЌЯрзВЪБдкЪ§жсЩЯЫљЖдгІЕФЪ§ЪЧ-32.
ЧђДњБэЕФЪ§ЪЧ100ЃЛЃЈ2ЃЉЂй40ЃЛ-50ЃЛ40ЃЌ-70ЃЛЂкОЙ§16УыСНЧђЯрзВЃЌЯрзВЪБдкЪ§жсЩЯЫљЖдгІЕФЪ§ЪЧ-32.
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШПЩвдМЦЫуГіACЕФОрРы![]() ЃЌдйИљОнЫќдкИКАыжсЩЯаДГіЫќБэЪОЕФЪ§ЃЌМЦЫуГіAEЕФГЄЃЌдйИљОнЫќдке§АыжсЩЯЃЌдђПЩаДГіЫќБэЪОЕФЪ§ЃЛ
ЃЌдйИљОнЫќдкИКАыжсЩЯаДГіЫќБэЪОЕФЪ§ЃЌМЦЫуГіAEЕФГЄЃЌдйИљОнЫќдке§АыжсЩЯЃЌдђПЩаДГіЫќБэЪОЕФЪ§ЃЛ
ЃЈ2ЃЉЂйИљОнЬтвтЃЌAЧђвЛИіРДЛизмТЗГЬЮЊ(180ЁС2)cmЃЌЯдШЛДЫЪБзмТЗГЬЪЧ180ЁС2+40ЃЌдйИљОнЪБМф=ТЗГЬЁТЫйЖШНјааМЦЫуЃЛОЙ§ 63 УыЪБЃЌAЧђдЫЖЏЕФзмТЗГЬЮЊ![]() ЃЌРыЛиЕНдЕуЛЙВю90cmЃЌОнДЫПЩвдзїД№ЃЛ
ЃЌРыЛиЕНдЕуЛЙВю90cmЃЌОнДЫПЩвдзїД№ЃЛ
ЂкЩшОЙ§![]() УыСНЧђЯрзВЃЌвРЬтвтСаЪНМЦЫуМДПЩ.
УыСНЧђЯрзВЃЌвРЬтвтСаЪНМЦЫуМДПЩ.
ЃЈ1ЃЉвРЬтвтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
гжЁпCдкИКАыжсЃЌEе§АыжсЃЌ
ЁрCДњБэ![]() ЃЌEДњБэ
ЃЌEДњБэ![]() ЃЎ
ЃЎ
ЙЪ![]() ЧђДњБэЕФЪ§ЪЧ-50ЃЌ
ЧђДњБэЕФЪ§ЪЧ-50ЃЌ![]() ЧђДњБэЕФЪ§ЪЧ100ЃЛ
ЧђДњБэЕФЪ§ЪЧ100ЃЛ
ЃЈ2ЃЉЂйИљОнЬтвтЃЌAЧђвЛИіРДЛизмТЗГЬЮЊ(180ЁС2)cmЃЌAЧђЕкЖўДЮЕНДя![]() ЧђЫљдкЮЛжУЪБгУСЫ
ЧђЫљдкЮЛжУЪБгУСЫ![]() (Уы)ЃЛ
(Уы)ЃЛ
ОЙ§ 63 УыЪБЃЌAЧђдЫЖЏЕФзмТЗГЬЮЊ![]() (
(![]() )ЃЌЫљвдРыЕкЖўИіРДЛиЛиЕНдЕуЯрВюЃК
)ЃЌЫљвдРыЕкЖўИіРДЛиЛиЕНдЕуЯрВюЃК![]() ЃЌДЫЪБ AЧђЭЃдкдCЧђЕФЮЛжУЃЌдкЪ§жсЩЯЫљЖдгІЕФЪ§ЮЊ
ЃЌДЫЪБ AЧђЭЃдкдCЧђЕФЮЛжУЃЌдкЪ§жсЩЯЫљЖдгІЕФЪ§ЮЊ![]() ЃЛBЧђЭЃдкдAЧђЕФЮЛжУЃЌдкЪ§жсЩЯЫљЖдгІЕФЪ§ЮЊ
ЃЛBЧђЭЃдкдAЧђЕФЮЛжУЃЌдкЪ§жсЩЯЫљЖдгІЕФЪ§ЮЊ![]() ЃЛCЧђЛЙдкдЫЖЏдкжЎжаРыDЛЙга10cmЃЌдкЪ§жсЩЯЫљЖдгІЕФЪ§ЮЊ
ЃЛCЧђЛЙдкдЫЖЏдкжЎжаРыDЛЙга10cmЃЌдкЪ§жсЩЯЫљЖдгІЕФЪ§ЮЊ![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊЃК40ЃЛ-50ЃЛ40ЃЌ-70ЃЛ
ЂкЩшОЙ§![]() УыСНЧђЯрзВЃЌИљОнЬтвтЕУ
УыСНЧђЯрзВЃЌИљОнЬтвтЕУ
![]()
НтЕУЃК![]()
![]()
Д№ЃКОЙ§16УыСНЧђЯрзВЃЌЯрзВЪБдкЪ§жсЩЯЫљЖдгІЕФЪ§ЪЧ-32.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
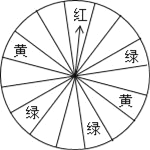
ЁОЬтФПЁПЁАСљвЛЁБЖљЭЏНкЦкМфЃЌФГЩЬЯУЮЊСЫЮќв§ЙЫПЭЃЌЩшСЂСЫвЛИіПЩвдздгЩзЊЖЏЕФзЊХЬЃЈзЊХЬБЛЦНОљЗжГЩ16ЗнЃЉЃЌВЂЙцЖЈЃКЙЫПЭУПЙКТђ100дЊЕФЩЬЦЗЃЌОЭФмЛёЕУвЛДЮзЊЖЏзЊХЬЕФЛњЛсЃЎШчЙћзЊХЬЭЃжЙКѓЃЌжИеые§КУЖдзМФФИіЧјгђЃЌЙЫПЭОЭПЩвдЛёЕУЯргІЕФНБЦЗЃЎ
беЩЋ | НБЦЗ |
КьЩЋ | ЭцОпам |
ЛЦЩЋ | ЭЏЛАЪщ |
ТЬЩЋ | ВЪБЪ |
аЁУїКЭТшТшЙКТђСЫ125дЊЕФЩЬЦЗЃЌЧыФуЗжЮіМЦЫуЃК
(1)аЁУїЛёЕУНБЦЗЕФИХТЪЪЧЖрЩйЃП
(2)аЁУїЛёЕУЭЏЛАЪщЕФИХТЪЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌЕу
жаЃЌЕу![]() ЗжБ№дкБп
ЗжБ№дкБп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЎЯТСаЫФИіХаЖЯжаЃЌВЛе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
ЃЎЯТСаЫФИіХаЖЯжаЃЌВЛе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ

A. ЫФБпаЮ![]() ЪЧЦНааЫФБпаЮ
ЪЧЦНааЫФБпаЮ
B. ШчЙћ![]() ЃЌФЧУДЫФБпаЮ
ЃЌФЧУДЫФБпаЮ![]() ЪЧОиаЮ
ЪЧОиаЮ
C. ШчЙћ![]() ЦНЗжЦНЗжЁЯBACЃЌФЧУДЫФБпаЮ AEDF ЪЧСтаЮ
ЦНЗжЦНЗжЁЯBACЃЌФЧУДЫФБпаЮ AEDF ЪЧСтаЮ
D. ШчЙћADЁЭBC Чв ABЃНACЃЌФЧУДЫФБпаЮ AEDF ЪЧе§ЗНаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ1ЃЌЁїABCжаЃЌЁЯC=90ЁуЃЌABЕФДЙжБЦНЗжЯпНЛACгкЕуDЃЌСЌНгBD. ШєAC=2ЃЌBC=1ЃЌдђЁїBCDЕФжмГЄЮЊ___________________.
ЃЈ2ЃЉOЮЊе§ЗНаЮABCDЕФжааФЃЌEЮЊCDБпЩЯвЛЕуЃЌFЮЊADБпЩЯвЛЕуЃЌЧвЁїEDFЕФжмГЄЕШгкADЕФГЄ.
ЂйдкЭМ2жаЧѓзїЁїEDF.ЃЈвЊЧѓЃКГпЙцзїЭМЃЌВЛаДзїЗЈЃЌБЃСєзїЭМКлМЃЃЉ
ЂкдкЭМ3жаВЙШЋЭМаЮЃЌЧѓЁЯEOFЕФЖШЪ§.
ЂлШє![]() ЃЌдђ
ЃЌдђ![]() =_______________.
=_______________.

ЭМ1 ЭМ2 ЭМ3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкШчЭМЕФ2017Фъ11дТЗнЕФдТРњБэжаЃЌШЮвтПђГіБэжаЪњСаЩЯШ§ИіЯрСкЕФЪ§ЃЌетШ§ИіЪ§ЕФКЭВЛПЩФмЪЧЃЈЁЁЁЁЃЉ
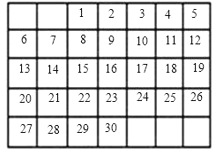
A.27B.51
C.69D.72
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫу
ЃЈ1ЃЉ![]() ЃЈ2ЃЉ
ЃЈ2ЃЉ![]()
ЃЈ3ЃЉЃЈ2![]() Љ
Љ![]() ЃЉ2+ЃЈ
ЃЉ2+ЃЈ![]() +2
+2![]() ЃЉЁТ
ЃЉЁТ![]() ЃЎ
ЃЎ
ЃЈ4ЃЉ![]() ЉЃЈ
ЉЃЈ![]() ЃЉЉ1+
ЃЉЉ1+![]() ЃЈ
ЃЈ![]() Љ1ЃЉЉ20180Љ|
Љ1ЃЉЉ20180Љ|![]() Љ2|ЃЎ
Љ2|ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫЗсИЛЩйФъЖљЭЏЕФвЕгрЩњЛюЃЌФГЩчЧјвЊдкШчЭМЫљЪОABЫљдкЕФжБЯпНЈвЛЭМЪщЪвЃЌБОЩчЧјгаСНЫљбЇаЃЫљдкЕФЮЛжУдкЕуCКЭЕуDДІЃЌCAЁЭABгкAЃЌDBЁЭABгкBЃЌвбжЊABЃН25kmЃЌCAЃН15kmЃЌDBЃН10kmЃЌЪдЮЪЃКЭМЪщЪвEгІИУНЈдкОрЕуAЖрЩйkmДІЃЌВХФмЪЙЫќЕНСНЫљбЇаЃЕФОрРыЯрЕШ?

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЯпЖЮAB=![]() (
(![]() ЮЊГЃЪ§)ЃЌЕуCЮЊжБЯпABЩЯвЛЕуЃЌЕуPЁЂQЗжБ№дкЯпЖЮBCЁЂACЩЯЃЌЧвТњзуCQ=2AQЃЌCP=2BP.
ЮЊГЃЪ§)ЃЌЕуCЮЊжБЯпABЩЯвЛЕуЃЌЕуPЁЂQЗжБ№дкЯпЖЮBCЁЂACЩЯЃЌЧвТњзуCQ=2AQЃЌCP=2BP.
(1)ШчЭМЃЌЕБЕуCЧЁКУдкЯпЖЮABжаЕуЪБЃЌдђPQ=_______(гУКЌ![]() ЕФДњЪ§ЪНБэЪО)ЃЛ
ЕФДњЪ§ЪНБэЪО)ЃЛ
(2)ШєЕуCЮЊжБЯпABЩЯШЮвЛЕуЃЌдђPQГЄЖШЪЧЗёЮЊГЃЪ§?ШєЪЧЃЌЧыЧѓГіетИіГЃЪ§ЃЛШєВЛЪЧЃЌЧыЫЕУїРэгЩЃЛ
(3)ШєЕуCдкЕуAзѓВрЃЌЭЌЪБЕуPдкЯпЖЮABЩЯ(ВЛгыЖЫЕужиКЯ)ЃЌЧыХаЖЯ2AP+CQ-2PQгы1ЕФДѓаЁЙиЯЕЃЌВЂЫЕУїРэгЩЁЃ
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2ЬЈДѓЪеИюЛњКЭ5ЬЈаЁЪеИюЛњЭЌЪБЙЄзї2 hЙВЪеИюаЁТѓ3.6hm2ЃЌ3ЬЈДѓЪеИюЛњКЭ2ЬЈаЁЪеИюЛњЭЌЪБЙЄзї5 hЙВЪеИюаЁТѓ8 hm2.1ЬЈДѓЪеИюЛњКЭ1ЬЈаЁЪеИюЛњУПаЁЪБИїЪеИюаЁТѓЖрЩйЙЋЧъ?
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com