
【题目】计算
(1)![]() (2)
(2)![]()
(3)(2![]() ﹣
﹣![]() )2+(
)2+(![]() +2
+2![]() )÷
)÷![]() .
.
(4)![]() ﹣(
﹣(![]() )﹣1+
)﹣1+![]() (
(![]() ﹣1)﹣20180﹣|
﹣1)﹣20180﹣|![]() ﹣2|.
﹣2|.
【答案】(1)6;(2)1;(3)![]() ;(4)
;(4) ![]() .
.
【解析】
(1)利用平方差公式计算即可;
(2)原式第一项化为最简二次根式,第二项根据绝对值的意义化简,第三项根据零指数幂计算,第四项根据乘方法则计算后合并即可;
(3)原式第一项利用完全平方公式展开,利用多项式除以单项式的方法把第二项变形,最后合并而成根式即可;
(4)原式第一项化为最简二次根式,第二项根据负整数指数幂计算,第三项根据乘法分配律展开,第三项根据零指数幂计算,第五项去绝对值号计算后合并即可.
(1)![]() =(
=(![]() )2-(
)2-(![]() )2=12-6=6;
)2=12-6=6;
(2)![]() =3
=3![]() -2
-2![]() -
-![]() +1=1;
+1=1;
(3)(2![]() ﹣
﹣![]() )2+(
)2+(![]() +2
+2![]() )÷
)÷![]() =12+6-12
=12+6-12![]() +3
+3![]() +2
+2![]() =18-7
=18-7![]() ;
;
(4)![]() ﹣(
﹣(![]() )﹣1+
)﹣1+![]() (
(![]() ﹣1)﹣20180﹣|
﹣1)﹣20180﹣|![]() ﹣2|=2
﹣2|=2![]() -
-![]() +3-
+3-![]() -1-2+
-1-2+![]() =
=![]() .
.


科目:初中数学 来源: 题型:
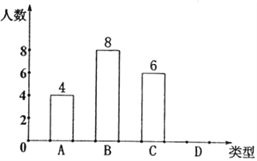
【题目】某校260名学生参加献爱心捐款活动,每人捐款4~7元,活动结束后随机抽查了20名学生每人的捐款数量,并按每人的捐款数量分为四种类型,A:捐款4元;B:捐款5元;C:捐款6元;D:捐款7元,并将其绘成如图所示的条形统计图.
(1)通过计算补全条形统计图;
(2)直接写出这20名学生每人捐款数量的众数和中位数;
(3)求这20名学生每人捐款数量的的平均数,并估计260名学生共捐款多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校为了创建“书香校园”,购买了一批图书,其中科普类图书平均每本的 价格比文学类图书平均每本的价格多4元,已知学校用16000元购买的科普类图书的本数与用12000元购买的文学类图书的本数相等.求学校购买的科普类图书和文学类图书平均每本的价格各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个直角三角形的直角顶点重合,∠AOC=40°,求∠BOD 的度数.
结合图形,完成填空:
解法 1:
因为![]() ,
,![]()
所以![]()
![]()
因为![]()
![]()
所以![]()
![]()
![]()
所以![]()
![]()
解法2:
因为![]()
![]() ,
,![]()
![]() ,①
,①
所以![]() .②
.②
因为![]()
所以![]()
![]()
在上面①到②的推导过程中,理由依据是: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个“磁悬浮”的轨道架上做钢球碰撞实验,如图 1 所示,轨道长为 180![]() ,轨道架上有三个大小、质量完全相同的钢球
,轨道架上有三个大小、质量完全相同的钢球![]() 、
、![]() 、
、![]() ,轨道左右各有一个钢制挡板
,轨道左右各有一个钢制挡板 ![]() 和
和 ![]() ,其中
,其中![]() 到左挡板的距离为 30
到左挡板的距离为 30![]() ,
,![]() 到右挡板的距离为 60
到右挡板的距离为 60![]() ,
,![]() 、
、![]() 两球相距40
两球相距40![]() .现以轨道所在直线为数轴,假定
.现以轨道所在直线为数轴,假定![]() 球在原点,
球在原点,![]() 球代表的数为 40,如图 2 所示,解答下列问题:
球代表的数为 40,如图 2 所示,解答下列问题:

(1)在数轴上,找出 ![]() 球及右挡板
球及右挡板 ![]() 所代表的数,并填在图中括号内.
所代表的数,并填在图中括号内.

(2)碰撞实验中(钢球大小、相撞时间不记),钢球的运动都是匀速,当一钢球以一速度撞向另一静止钢球时,这个钢球停留在被撞钢球的位置,被撞钢球则以同样的速度向前运动,钢球撞到左右挡板则以相同的速度反向运动.
①现 ![]() 球以每秒 10
球以每秒 10![]() 的速度向右匀速运动,则
的速度向右匀速运动,则 ![]() 球第二次到达
球第二次到达![]() 球所在位置时用了 秒;经过 63 秒时,
球所在位置时用了 秒;经过 63 秒时,![]() 、
、![]() 、
、![]() 三球在数轴上所对应的数分别是 、 、 ;
三球在数轴上所对应的数分别是 、 、 ;
②如果![]() 、
、![]() 两球同时开始运动,
两球同时开始运动,![]() 球向左运动,
球向左运动,![]() 球向右运动,
球向右运动,![]() 球速度是每秒 8
球速度是每秒 8![]() ,
,![]() 球速度是每秒 12
球速度是每秒 12![]() ,问:经过多少时间
,问:经过多少时间 ![]() 、
、![]() 两球相撞?相撞时在数轴上所对应的数是多少?
两球相撞?相撞时在数轴上所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市要销售一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)求销售单价为多少元时,该文具每天的销售利润最大,并求出最大的利润;
(2)经过试营销后,超市按(1)中单价销售,为了回馈广大顾客,同时提高该文具知名度,超市决定在1月1日当天开展降价促销活动,若每件文具降价2a%,则可多售出4a%,结果当天销售额为5670元,要使销量尽可能地大,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示.

(1)补充完成下面的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 | 3.41 | 90% | 20% | |
乙组 | 7.5 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板的两直角边所在直线分别与直线BC,CD交于点M,N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是__________________;
(2)如图2,若点O在正方形的中心(即两对角线的交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说理)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》卷九“勾股”中记载:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问霞长几何.
注释:今有正方形水池边长1丈,芦苇生长在中央,长出水面1尺.将芦苇向池岸牵引,恰好与水岸齐,问芦苇的长度(一丈等于10尺).解决下列问题:
(1)示意图中,线段![]() 的长为______尺,线段
的长为______尺,线段![]() 的长为______尺;
的长为______尺;

(2)求芦苇的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com