
����Ŀ����ƽ��ֱ������ϵ�У����κ���![]() ��ͼ����
��ͼ����![]() �ύ��A����3��0����B��1��0�����㣬��y�ύ�ڵ�C��
�ύ��A����3��0����B��1��0�����㣬��y�ύ�ڵ�C��

��1����������κ����Ľ���ʽ��
��2����P��ֱ��AC�Ϸ�����������һ���㣬�Ƿ���ڵ�P��ʹ��ACP�������������ڣ������P�����ꣻ�������ڣ�˵�����ɣ�
��3����Q��ֱ��AC�Ϸ�����������һ���㣬����Q��QE��ֱ��![]() �ᣬ����ΪE���Ƿ���ڵ�Q��ʹ�Ե�B��Q��EΪ���������������AOC���ƣ������ڣ�ֱ��д����Q�����ꣻ�������ڣ�˵�����ɣ�
�ᣬ����ΪE���Ƿ���ڵ�Q��ʹ�Ե�B��Q��EΪ���������������AOC���ƣ������ڣ�ֱ��д����Q�����ꣻ�������ڣ�˵�����ɣ�
���𰸡���1��![]()
��2�����ڵ�![]() ��ʹ��ACP��������
��ʹ��ACP��������
��3��������Q��������![]() ��
��![]()
��������
���������26���⣺��1����������![]() ����A����3��0����B��1��0����
����A����3��0����B��1��0����
��![]() ����������������������������������������������1��
����������������������������������������������1��
��� ��������������������������������������������������2��
��������������������������������������������������2��
����κ����Ĺ�ϵ����ʽ![]() ����������������������3��
����������������������3��
��2������PO����PM��x����M��PN��y����N����4��
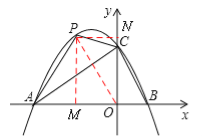
���P������m��n������![]() ��
��
PM =![]() ��
��![]() ��AO=3����5�֣�
��AO=3����5�֣�
��![]() ʱ��
ʱ��![]() ������
������
��OC=2������������������������������������������������6��
![]() ��
��![]()
��![]() ��
��![]() ��8��
��8��
��![]() ��������0���൱
��������0���൱![]() ʱ������
ʱ������![]()
![]() �����ֵ��
�����ֵ��
��ʱ![]()
![]() ��
��![]() �� ��������9��
�� ��������9��
����ڵ�![]() ��ʹ��ACP���������� ����������������������10��
��ʹ��ACP���������� ����������������������10��
��3��������Q��������![]() ��
��![]() ��������������������������12��
��������������������������12��
�֡�BQE�ס�AOC����EBQ�ס�AOC����QEB�ס�AOC����������ۿ��ó���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
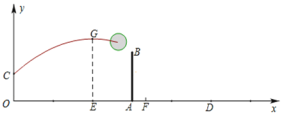
����Ŀ����2016�������Լ���˻��ϣ��й�Ů�ſ˷��������ѣ�ƾ����ǿ�������ͳ�ǿ��ʵ���Ⱥ�սʤ��ʵ��ͬ����ǿ�İ����ӣ������Ӻ�����ά�Ƕӣ�����˰��˹ھ���Ϊ������������˹⣮
��ͼ����֪Ů���ij���ODΪ18�ף�λ�������ߴ�������AB�ĸ߶�Ϊ2.24�ף�һ��Ավ�ڵ�O����������ӵ�O�����Ϸ�2��C������ǰ����ȥ������ķ���·���������ߵ�һ���֣����������������O��ˮƽ����OEΪ6��ʱ��������ߵ�F����OΪԭ�㽨����ͼ��ʾ��ƽ��ֱ������ϵ��
��1�����������е����߶�Ϊ2.8��ʱ����������еĸ߶�y����λ���ף���ˮƽ����x����λ���ף�֮��ĺ�����ϵʽ��
��2���ڣ�1���������£�������������ܹ�����������ܹ��������Ƿ����磿��˵�����ɣ�
��3��ϲ�������������ͬѧ���о����֣�����Ҫ������������е����߶�h���ף�Ӧ����h��2.32����������֪�����ȷ��h��ȡֵ��Χ��ʹ������磨����ѹ������û���磩�������æ�����ָ��ʹ����ܹ����ֲ�������h��ȡֵ��Χ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ÿ���������ľ���Ϊһ����λ���ȣ���![]() ��
��![]() ��
��![]() ��
��![]() ��Ӧ�����ֱ���
��Ӧ�����ֱ���![]() ����
����![]() .
.
��1����ô![]() ��
��![]() ��
��
��2����![]() ��
��![]() ����λ/����ٶ�����������������˶���
����λ/����ٶ�����������������˶���![]() ����
����![]() ��
��![]() ����λ/����ٶ�Ҳ����������������˶�������
����λ/����ٶ�Ҳ����������������˶�������![]() �����
�����![]() �����̷��أ����
�����̷��أ����![]() �������ij�㴦��������������Ӧ������
�������ij�㴦��������������Ӧ������
��3�����![]() ��
��![]() �����ԣ�2���е��ٶ�ͬʱ������ĸ������˶�����
�����ԣ�2���е��ٶ�ͬʱ������ĸ������˶�����![]() ��ͼ�ϵ�λ�ó���Ҳ������ĸ������˶�����ʼ�ձ���
��ͼ�ϵ�λ�ó���Ҳ������ĸ������˶�����ʼ�ձ���![]() ������
������![]() �˶���
�˶���![]() ʱ����
ʱ����![]() ��Ӧ�����Ƕ��٣�
��Ӧ�����Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ij�Ϊ6����Ϊ4����������������ƽ��2����λ��������ƽ��2����λ�õ�������![]() ������Ӱ���������( )
������Ӱ���������( )
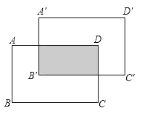
A.12B.10C.8D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��+3+(-5)
��2��-89-11
��3������5.5��+����3.2��������2.5����4.8
��4��17������8��������2��+4������3��
��5������32![]() ������5
������5![]() ������3
������3![]() ��������5
��������5![]() ��������2
��������2![]() ����
����
��6����![]() ��������12��
��������12��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������ֱ�ߵ�·��ͬ��㡢ͬ�յ㡢ͬ���ֱ��Բ�ͬ���ٶ�������1500�ף��ȵ��յ����ԭ����Ϣ����֪���ȳ���30����Ҳų����������ܲ������������У��ס������˵ľ���y���ף���׳�����ʱ��x���룩֮��Ĺ�ϵ��ͼ��ʾ�����ҵ��յ�ʱ�����յ�ľ����ǣ� ����

A. 150 B. 175 C. 180 D. 225
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����ABC=��ADC=90�����Խ���AC��BD���ڵ�O��DEƽ�֡�ADC��BC�ڵ�E������OE��
��1����֤���ı���ABCD�Ǿ��Σ�
��2����AB=2������OEC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
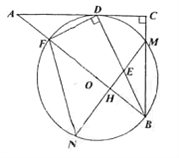
����Ŀ����ͼ����Rt��ABC�У���C=90����DΪAC��һ�㣬����BD��DF��BD��AB�ڵ�F����BDF�����Բ��O���BC����ڵ�M����AC�����ڵ�D������M��AB�Ĵ��߽�BD�ڵ�E������O�ڵ�N����AB�ڵ�H������FN.
��1����֤��BDƽ�֡�ABC��
��2������FM��BD�ཻ�ڵ�K����֤��MK=ME��
��3����AF=1��tan��N=![]() ����BE�ij�.
����BE�ij�.
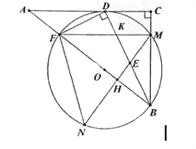
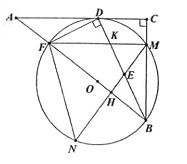
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ɱ߳�Ϊ1��С��������ɵ�����ͼ����һ�����������ABC����ע��������������߽��㴦�������γ�Ϊ��������Σ�
��1����ֱ��д��sin��ABC��ֵ�� ��
��2������ͼ�л����������DEF��ʹ����DEF�ס�ABC�������Ʊ�Ϊ2��1��
��3������ͼ��ȷ�����M��ʹ����BCM�����Ϊ6�������������ĸ��M��ֹһ������ֱ���M1��M2��M3����ʾ��
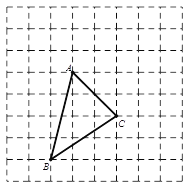
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com