
【题目】如图,在数轴上每相邻两点间的距离为一个单位长度,点![]() 、
、![]() 、
、![]() 、
、![]() 对应的数分别是
对应的数分别是![]() ,且
,且![]() .
.
(1)那么![]() ,
,![]() :
:
(2)点![]() 以
以![]() 个单位/秒的速度沿着数轴的正方向运动,
个单位/秒的速度沿着数轴的正方向运动,![]() 秒后点
秒后点![]() 以
以![]() 个单位/秒的速度也沿着数轴的正方向运动,当点
个单位/秒的速度也沿着数轴的正方向运动,当点![]() 到达点
到达点![]() 处立刻返回,与点
处立刻返回,与点![]() 在数轴的某点处相遇,求这个点对应的数;
在数轴的某点处相遇,求这个点对应的数;
(3)如果![]() 、
、![]() 两点以(2)中的速度同时向数轴的负方向运动,点
两点以(2)中的速度同时向数轴的负方向运动,点![]() 从图上的位置出发也向数轴的负方向运动,且始终保持
从图上的位置出发也向数轴的负方向运动,且始终保持![]() ,当点
,当点![]() 运动到
运动到![]() 时,点
时,点![]() 对应的数是多少?
对应的数是多少?

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知函数y=ax2-2ax-1(a是常数,a≠0),下列结论正确的是( )
A. 当a=1时,函数图象过点(-1,1)
B. 当a=-2时,函数图象与x轴没有交点
C. 若a>0,则当x≥1时,y随x的增大而减小
D. 若a<0,则当x≤1时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明解方程![]() 的过程,请你仔细阅读,并解答所提出的问题:
的过程,请你仔细阅读,并解答所提出的问题:
解:去括号,得
![]() . (第一步)
. (第一步)
移项,得
![]() . (第二步)
. (第二步)
合并同类项,得
![]() . (第三步)
. (第三步)
系数化为1,得
![]() . (第四步)
. (第四步)
(1)该同学解答过程从第_____步开始出错,错误原因是______________________;
(2)写出正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
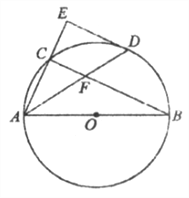
【题目】如图,△ABC内接于⊙O,AB为直径,点D在⊙O上,过点D作⊙O切线与AC的延长线交于点E,ED∥BC,连接AD交BC于点F.
(1)求证:∠BAD=∠DAE;
(2)若AB=6,AD=5,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车一天下午以车站为出发地在东西方向的大街上营运,规定向东为正,向西为负,行车里程(单位:![]() )依先后次序记录如下:
)依先后次序记录如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,+10.
,+10.
(1)将最后一名乘客送到目的地,出租车离车站出发点多远?在车站的什么方向?
(2)出租车在行驶过程中,离车站最远的距离是多少?
(3)出租车按物价部门规定,起步价(不超过![]() 千米)为
千米)为![]() 元,超过3千米的部分每千米的价格为
元,超过3千米的部分每千米的价格为![]() 元,司机一个下午的营业额是多少?
元,司机一个下午的营业额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个形状、大小完全相同的含有![]() 、
、![]() 的直角三角板如图①放置,
的直角三角板如图①放置,![]() 、
、![]() 与直线
与直线![]() 重合,且三角板
重合,且三角板![]() 、三角板
、三角板![]() 均可绕点
均可绕点![]() 逆时针旋转.
逆时针旋转.
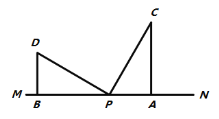
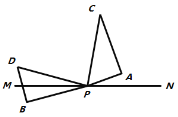
图① 图②
(1)直接写出![]() 的度数是______.
的度数是______.
(2)如图②,在图①基础上,若三角板![]() 的边
的边![]() 从
从![]() 处开始绕点
处开始绕点![]() 逆时针旋转,转速为4.5度/秒,同时三角板
逆时针旋转,转速为4.5度/秒,同时三角板![]() 的边
的边![]() 从
从![]() 处开始绕点
处开始绕点![]() 逆时针旋转,转速为0.5度/秒,(当
逆时针旋转,转速为0.5度/秒,(当![]() 转到与
转到与![]() 重合时,两三角板都停止转动),在旋转过程中,当
重合时,两三角板都停止转动),在旋转过程中,当![]() 与
与![]() 重合时,求旋转的时间是多少?
重合时,求旋转的时间是多少?
(3)在(2)的条件下,![]() 、
、![]() 、
、![]() 三条射线中,当其中一条射线平分另两条射线的夹角时,请求出旋转的时间.
三条射线中,当其中一条射线平分另两条射线的夹角时,请求出旋转的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程组解应用题
5月份,甲、乙两个工厂用水量共为200吨.进入夏季用水高峰期后,两工厂积极响应国家号召,采取节水措施.6月份,甲工厂用水量比5月份减少了15%,乙工厂用水量比5月份减少了10%,两个工厂6月份用水量共为174吨,求两个工厂5月份的用水量各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
轴交于A(-3,0),B(1,0)两点,与y轴交于点C.

(1)求这个二次函数的解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
(3)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于![]() 轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
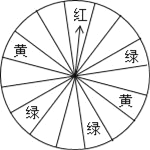
【题目】“六一”儿童节期间,某商厦为了吸引顾客,设立了一个可以自由转动的转盘(转盘被平均分成16份),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准哪个区域,顾客就可以获得相应的奖品.
颜色 | 奖品 |
红色 | 玩具熊 |
黄色 | 童话书 |
绿色 | 彩笔 |
小明和妈妈购买了125元的商品,请你分析计算:
(1)小明获得奖品的概率是多少?
(2)小明获得童话书的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com