
【题目】下面是小明解方程![]() 的过程,请你仔细阅读,并解答所提出的问题:
的过程,请你仔细阅读,并解答所提出的问题:
解:去括号,得
![]() . (第一步)
. (第一步)
移项,得
![]() . (第二步)
. (第二步)
合并同类项,得
![]() . (第三步)
. (第三步)
系数化为1,得
![]() . (第四步)
. (第四步)
(1)该同学解答过程从第_____步开始出错,错误原因是______________________;
(2)写出正确的解答过程.
科目:初中数学 来源: 题型:
【题目】如图,一个![]() 的方格图,由粗线隔为
的方格图,由粗线隔为![]() 个横竖各有
个横竖各有![]() 个格的“小九宫”格,其中,有一些方格填有
个格的“小九宫”格,其中,有一些方格填有![]() 至
至![]() 的数字,小鸣在第九行的空格中各填入了一个不大于
的数字,小鸣在第九行的空格中各填入了一个不大于![]() 的正整数,使每行、每列和每个“小九宫”格内的数字都不重复,然后小鸣将第九行的数字从左向右写成一个
的正整数,使每行、每列和每个“小九宫”格内的数字都不重复,然后小鸣将第九行的数字从左向右写成一个![]() 位数,这个
位数,这个![]() 位数是 __________.
位数是 __________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实素质教育要求,促进学生全面发展,我市某中学2016年投资11万元新增一批电脑,计划以后每年以相同的增长率进行投资,2018年投资18.59万元.
(1)求该学校为新增电脑投资的年平均增长率;
(2)从2016年到2018年,该中学三年为新增电脑共投资多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年巴西里约奥运会上,中国女排克服重重困难,凭借顽强的毅力和超强的实力先后战胜了实力同样超强的巴西队,荷兰队和塞尔维亚队,获得了奥运冠军,为祖国和人民争了光.
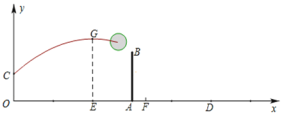
如图,已知女排球场的长度OD为18米,位于球场中线处的球网AB的高度为2.24米,一队员站在点O处发球,排球从点O的正上方2米的C点向正前方飞去,排球的飞行路线是抛物线的一部分,当排球运行至离点O的水平距离OE为6米时,到达最高点F,以O为原点建立如图所示的平面直角坐标系.
(1)当排球运行的最大高度为2.8米时,求排球飞行的高度y(单位:米)与水平距离x(单位:米)之间的函数关系式.
(2)在(1)的条件下,这次所发的球能够过网吗?如果能够过网,是否会出界?请说明理由.
(3)喜欢打排球的李明同学经研究后发现,发球要想过网,球运行的最大高度h(米)应满足h>2.32,但是他不知道如何确定h的取值范围,使排球不会出界(排球压线属于没出界),请你帮忙解决并指出使球既能过网又不会出界的h的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
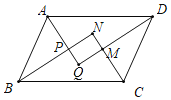
【题目】如图,在平行四边形ABCD中,AQ、BN、CN、DQ分別是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AQ与BN相交于点P,CN与DQ相交于点M,判断四边形MNPQ的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为1个单位,运动时间为t秒.过点P作PE⊥AO交AB于点E.
(1)求直线AB的解析式;
(2)设△PEQ的面积为S,求S与t时间的函数关系,并指出自变量t的取值范围;
(3)在动点P、Q运动的过程中,点H是矩形AOBC内(包括边界)一点,且以B、Q、E、H为顶点的四边形是菱形,直接写出t值和与其对应的点H的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,移动电商发展迅速,以下是2017年某调查机构发布的相关的统计表和统计图的一部分。请根据以上信息解答下列问题:

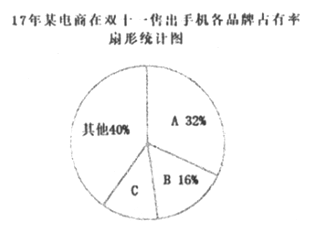
(1)2017年10月“移动电商行业用户规模”是___________亿台(结果精确到0.1亿台);并补全条形统计图;
(2)2017年10—12这三个月“移动电商行业用户规模”比上个月增长台数的平均数为___________亿台,若按此平均数增长,请你估计2018年1月“移动电商行业用户规模”为___________亿台(结果精确到0.1亿台);
(3)2017年某电商在双十一共售出手机12000台,则C品牌手机售出的台数是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上每相邻两点间的距离为一个单位长度,点![]() 、
、![]() 、
、![]() 、
、![]() 对应的数分别是
对应的数分别是![]() ,且
,且![]() .
.
(1)那么![]() ,
,![]() :
:
(2)点![]() 以
以![]() 个单位/秒的速度沿着数轴的正方向运动,
个单位/秒的速度沿着数轴的正方向运动,![]() 秒后点
秒后点![]() 以
以![]() 个单位/秒的速度也沿着数轴的正方向运动,当点
个单位/秒的速度也沿着数轴的正方向运动,当点![]() 到达点
到达点![]() 处立刻返回,与点
处立刻返回,与点![]() 在数轴的某点处相遇,求这个点对应的数;
在数轴的某点处相遇,求这个点对应的数;
(3)如果![]() 、
、![]() 两点以(2)中的速度同时向数轴的负方向运动,点
两点以(2)中的速度同时向数轴的负方向运动,点![]() 从图上的位置出发也向数轴的负方向运动,且始终保持
从图上的位置出发也向数轴的负方向运动,且始终保持![]() ,当点
,当点![]() 运动到
运动到![]() 时,点
时,点![]() 对应的数是多少?
对应的数是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com