
【题目】如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD与CE相交于点O,且BD=CE,连接AO.

(1)求证:△BOC是等腰三角形;
(2)求证:AO平分∠BAC.
【答案】(1)见解析 (2)见解析
【解析】
(1)根据BD⊥AC于点D,CE⊥AB于点E,利用HL定理得到Rt△BDC≌Rt△CEB,进一步得出∠DBC=∠ECB,由等角对等边得到OB=OC,即可解答;
(2)根据角平分线的判定定理,只需证明OD=OE即可.
证明:(1)∵BD⊥AC于点D,CE⊥AB于点E,
∴∠BDC=∠CEB=90°,
在Rt△BDC与Rt△CEB中![]() ,
,
∴Rt△BDC≌Rt△CEB(HL),
∴∠DBC=∠ECB,
∴OB=OC,
∴△BOC是等腰三角形;
(2)∵BD=CE,OB=OC,
∴BD﹣OB=CE﹣OC,
即OD=OE,
∵BD⊥AC,CE⊥AB,
∴AO平分∠BAC.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.求:
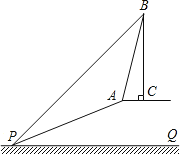
(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M.
(1)求∠E的度数.
(2)求证:M是BE的中点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国流传了上千年的传统节日,全国各地举行了丰富多彩的纪念活动,为了继承传统,减缓学生考前的心理压力,某班学生组织了一次拔河比赛,裁判员让两队队长用“石头、剪刀、布”的手势方式选择场地位置,规则是:石头胜剪刀,剪刀胜布,布胜石头,手势相同则再决胜负.
(1)用列表或画树状图法,列出甲、乙两队手势可能出现的情况;
(2)裁判员的这种做法对甲、乙双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边 且BE=CF,AD+EC=AB.

(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个计算器,计算![]() 时只能显示1.41421356237十三位(包括小数点),现在想知道7后面的数字是什么,可以在这个计算器中计算下面哪一个值( )
时只能显示1.41421356237十三位(包括小数点),现在想知道7后面的数字是什么,可以在这个计算器中计算下面哪一个值( )
A. 10![]() B. 10(
B. 10(![]() -1) C. 100
-1) C. 100![]() D.
D. ![]() -1
-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车制造厂开发了一款新式自行车,计划![]() 月份生产安装
月份生产安装![]() 辆,由于抽调不出足够的熟练工来完成新式自行车的安装,工厂决定招聘一些新工人;他们经过培训后也能独立进行安装.调研部门发现:
辆,由于抽调不出足够的熟练工来完成新式自行车的安装,工厂决定招聘一些新工人;他们经过培训后也能独立进行安装.调研部门发现: ![]() 名熟练工和
名熟练工和![]() 名新工人每日可安装辆自行车;
名新工人每日可安装辆自行车; ![]() 名熟练工和
名熟练工和![]() 名新工人每日可安装
名新工人每日可安装![]() 辆自行车。
辆自行车。
(1)每名熟练工和新工人每日分别可以安装多少辆自行车?
(2)如果工厂招聘![]() 名新工人(
名新工人(![]() ).使得招聘的新工人和抽调熟练工刚好能完成
).使得招聘的新工人和抽调熟练工刚好能完成![]() 月份(
月份(![]() 天)的安装任务,那么工厂有哪几种新工人的招聘方案?
天)的安装任务,那么工厂有哪几种新工人的招聘方案?
(3)该自行车关于轮胎的使用有以下说明:本轮胎如安装在前轮,安全行使路程为![]() 千公里;如安装在后轮,安全行使路程为
千公里;如安装在后轮,安全行使路程为![]() 千公里.请问一对轮胎能行使的最长路程是多少千公里?
千公里.请问一对轮胎能行使的最长路程是多少千公里?
查看答案和解析>>
科目:初中数学 来源: 题型:
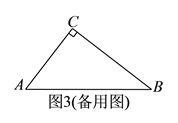
【题目】(![]() 分)如图,在
分)如图,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在边
在边![]() 上运动,
上运动, ![]() 平分
平分![]() 交边
交边![]() 于点
于点![]() ,
, ![]() 垂足为
垂足为![]() ,
, ![]() 垂足为
垂足为![]() .
.


(![]() )当
)当![]() 时,求证:
时,求证: ![]() .
.
(![]() )探究:
)探究: ![]() 为何值时,
为何值时, ![]() 与
与![]() 相似?
相似?
(![]() )直接写出:
)直接写出: ![]() __________时,四边形
__________时,四边形![]() 与
与![]() 的面积相等.
的面积相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知一次函数![]() ,
,
(1)无论 k为何值,函数图像必过定点,求该点的坐标;
(2)如图 1,当 k=-![]() 时,该直线交 x 轴,y 轴于 A,B 两点,直线 l2:y=x+1 交 AB 于点 P,点 Q 是 l2 上一点,若 SABQ 6 ,求 Q 点的坐标;
时,该直线交 x 轴,y 轴于 A,B 两点,直线 l2:y=x+1 交 AB 于点 P,点 Q 是 l2 上一点,若 SABQ 6 ,求 Q 点的坐标;
(3)如图 2,在第 2 问的条件下,已知 D 点在该直线上,横坐标为 1,C 点在 x 轴负半轴, ABC=45 ,动点 M 的坐标为(a,a),求 CM+MD 的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com