
【题目】已知:如图,斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.求:
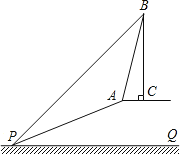
(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
【答案】(1)10m,(2)古塔BC的高度约为19米.
【解析】
试题分析:(1)过点A作AH⊥PQ,垂足为点H,利用斜坡AP的坡度为1:2.4,得出AH,PH,AP的关系求出即可;
(2)利用矩形性质求出设BC=x,则x+10=24+DH,再利用tan76°=![]() ,求出即可.
,求出即可.
试题解析:(1)过点A作AH⊥PQ,垂足为点H.
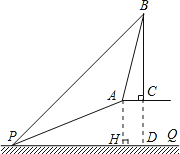
∵斜坡AP的坡度为1:2.4,
∴![]() ,
,
设AH=5km,则PH=12km,
由勾股定理,得AP=13km.
∴13k=26m. 解得k=2.
∴AH=10m.
答:坡顶A到地面PQ的距离为10m.
(2)延长BC交PQ于点D.
∵BC⊥AC,AC∥PQ,
∴BD⊥PQ.
∴四边形AHDC是矩形,CD=AH=10,AC=DH.
∵∠BPD=45°,
∴PD=BD.
设BC=x,则x+10=24+DH.∴AC=DH=x-14.
在Rt△ABC中,tan76°=![]() ,
,
即![]()
解得x=![]() ,即x≈19,
,即x≈19,
答:古塔BC的高度约为19米.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
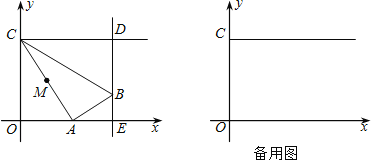
【题目】如图,在平面直角坐标系中,点C的坐标为(0,4),动点A以每秒1个单位长的速度,从点O出发沿x轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D.运动时间为t秒.
(1)当点B与点D重合时,求t的值;
(2)设△BCD的面积为S,当t为何值时,S=![]() ?
?
(3)连接MB,当MB∥OA时,如果抛物线y=ax2﹣10ax的顶点在△ABM内部(不包括边),求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).

(1)四边形EFGH的形状是_______,证明你的结论.
(2)连接四边形ABCD的对角线AC与BD,当AC与BD满足____条件时,四边形EFGH是矩形;(只需要写结论,不需证明)
(3)连接四边形ABCD的对角线AC与BD,当AC与BD满足______条件时,四边形EFGH是菱形.(只需要写结论,不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )

A.6cm2B.8 cm2C.10 cm2D.12 cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() ,分别根据下列条件求出点P的坐标.
,分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点P到x轴、y轴的距离相等;
(4)点Q的坐标为![]() ,直线
,直线![]() 轴.
轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店打出促销广告:最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交车每天的支出费用为600元每天的乘车人数x(人)与每天利润(利润=票款收入-支出费用)y(元)的变化关系如下表所示(每位乘客的乘车票价固定不变): 根据表格中的数据,回答下列问题:
x(人) | …… | 200 | 250 | 300 | 350 | 400 | …… |
y(元) | …… | -200 | -100 | 0 | 100 | 200 | …… |
(1)在这个变化关系中,自变量是什么?因变量是什么?
(2)若要不亏本,该公交车每天乘客人数至少达到多少?
(3)请你判断一天乘客人数为500人时利润是多少?
(4)试写出该公交车每天利润y(元)与每天乘车人数x(人)的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD与CE相交于点O,且BD=CE,连接AO.

(1)求证:△BOC是等腰三角形;
(2)求证:AO平分∠BAC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com