
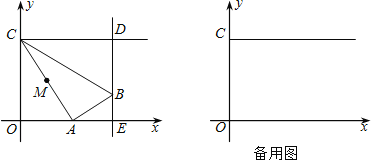
【题目】如图,在平面直角坐标系中,点C的坐标为(0,4),动点A以每秒1个单位长的速度,从点O出发沿x轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D.运动时间为t秒.
(1)当点B与点D重合时,求t的值;
(2)设△BCD的面积为S,当t为何值时,S=![]() ?
?
(3)连接MB,当MB∥OA时,如果抛物线y=ax2﹣10ax的顶点在△ABM内部(不包括边),求a的取值范围.
【答案】(1)t=8(2)当t=3或3+5![]() 时,S=
时,S=![]() (3)-
(3)-![]() <a<-
<a<-![]()
【解析】解:(1)∵![]() ,
,![]() ,
,
∴![]() .
.
∴Rt△CAO∽Rt△ABE.·························· 2分
∴![]() .
.
∴![]() .∴
.∴![]() .························· 3分
.························· 3分
(2)由Rt△CAO∽Rt△ABE可知:![]() ,
,![]() .··········· 4分
.··········· 4分
当0<![]() <8时,
<8时,![]() .
.
∴![]() .····························· 6分
.····························· 6分
当![]() >8时,
>8时,![]() .
.
∴![]() ,
,![]() (为负数,舍去).
(为负数,舍去).
当![]() 或
或![]() 时,
时,![]() .······················ 8分
.······················ 8分

(3)过M作MN⊥![]() 轴于N,则
轴于N,则![]() .
.
当MB∥OA时,![]() ,
,![]() .··············· 9分
.··············· 9分
抛物线![]() 的顶点坐标为(5,
的顶点坐标为(5,![]() ).············· 10分
).············· 10分
它的顶点在直线![]() 上移动.
上移动.
直线![]() 交MB于点(5,2),交AB于点(5,1).············· 11分
交MB于点(5,2),交AB于点(5,1).············· 11分
∴1<![]() <2.
<2.
∴![]() <
<![]() <
<![]() . 12分
. 12分


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
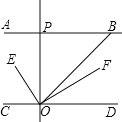
【题目】AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论: ①∠BOE=![]() (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A、B两点分别对应有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|,利用数形结合思想回答下列问题:
![]()
(1)数轴上表示2和10两点之间的距离是 ,数轴上表示2和﹣10两点之间的距离是 ;
(2)数轴上,x和﹣2两点之间的距离是 ;
(3)若x表示一个有理数,则|x﹣1|+|x+2|有最小值吗?若有,请求出最小值,若没有,写出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小李做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:

(1)请估计:当实验次数为5000次时,摸到白球的频率将会接近 ;(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(摸到白球)= ;
(3)试验估算这个不透明的盒子里黑球有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(-3,0),B(0,3),DA⊥x轴,点C在OA上且∠CDB=∠ OBD,则∠CBD的度数是( )
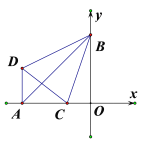
A.72°B.60°C.45°D.36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据全等多边形的定义,我们把四个角,四条边分别相等的两个凸四边形叫做全等四边形,记作:四边形ABCD≌四边形A1B1C1D1
(1)若四边形ABCD≌四边形A1B1C1D1,已知AB3,BC4,ADCD5,B90,D 60,则A1D1 ,B1 , A1C1 (直接写出答案);
(2)如图 1,四边形 ABEF≌四边形CBED,连接AD交 BE于点O,连接F,求证:AOBFOE;
(3)如图 2,若ABA1B1,BCB1C1,CDC1D1,ADA1D1,BB1,求证:四边形ABCD≌四边形A1B1C1D1


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是BC边上的一点,BE=4,EC=8,将正方形边AB延AE折叠刀AF,延长EF交DC于G,连接AG,现在有如下结论:①∠EAG=45°;②GC=CF;③FC∥AG;④S△GFC=14.4;其中结论正确的个数是( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个汽车零件制造车间可以生产甲,乙两种零件,生产4个甲种零件和3个乙种零件共获利120元;生产2个甲种零件和5个乙种零件共获利130元.
(1)求生产1个甲种零件,1个乙种零件分别获利多少元?
(2)若该汽车零件制造车间共有工人30名,每名工人每天可生产甲种零件6个或乙种零件5个,每名工人每天只能生产同一种零件,要使该车间每天生产的两种零件所获总利润超过2800元,至少要派多少名工人去生产乙种零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.求:
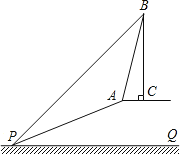
(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com