
ЎѕМвДїЎїЈЁ9·ЦЈ©ОЄЅшТ»ІЅНЖ№гЎ°Сф№вМеУэЎ±ґуїОјд»о¶ЇЈ¬ДіЦРС§¶ФТСїЄЙиµДAКµРДЗтЈ¬BБў¶ЁМшФ¶Ј¬CЕЬІЅЈ¬DМшЙюЛДЦЦ»о¶ЇПоДїµДС§ЙъПІ»¶ЗйїцЅшРРµчІйЈ¬Лж»ъійИЎБЛІї·ЦС§ЙъЈ¬ІўЅ«µчІйЅб№ы»жЦЖіЙНј1Ј¬Нј2µДНіјЖНјЈ¬ЗлЅбєПНјЦРµДРЕПўЅвґрПВБРОКМвЈє
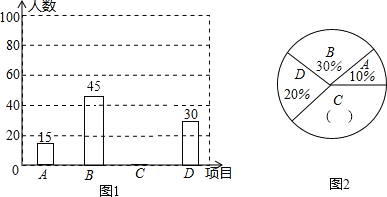
ЈЁ1Ј©ЗлјЖЛг±ѕґОµчІйЦРПІ»¶Ў°ЕЬІЅЎ±µДС§ЙъИЛКэєНЛщХј°Щ·Ц±ИЈ¬ІўЅ«БЅёцНіјЖНјІ№ідНкХыЈ»
ЈЁ2Ј©Лж»ъійИЎБЛ5ГыПІ»¶Ў°ЕЬІЅЎ±µДС§ЙъЈ¬ЖдЦРУР3ГыЕ®ЙъЈ¬2ГыДРЙъЈ¬ПЦґУХв5ГыС§ЙъЦРИОТвійИЎ2ГыС§ЙъЈ¬ЗлУГ»КчЧґНј»тБР±нµД·Ѕ·ЁЈ¬ЗуіцёХєГійµЅН¬РФ±рС§ЙъµДёЕВКЈ®
Ўѕґр°ёЎїЈЁ1Ј©60ЈЁИЛЈ©Ј¬40%Ј¬ЈЁ2Ј©![]() Ј®
Ј®
ЎѕЅвОцЎї
КФМвЈЁ1Ј©УГAµДИЛКэіэТФЛщХјµД°Щ·Ц±ИЈ¬јґїЙЗуіцµчІйµДС§ЙъКэЈ»УГійІйµДЧЬИЛКэјхИҐAЎўBЎўDµДИЛКэЈ¬ЗуіцПІ»¶Ў°ЕЬІЅЎ±µДС§ЙъИЛКэЈ¬ФЩіэТФ±»µчІйµДС§ЙъКэЈ¬ЗуіцЛщХјµД°Щ·Ц±ИЈ¬ФЩ»НјјґїЙЈ»
ЈЁ2Ј©УГA±нКѕДРЙъЈ¬B±нКѕЕ®ЙъЈ¬»іцКчРОНјЈ¬ФЩёщѕЭёЕВК№«КЅЅшРРјЖЛгјґїЙЈ®
КФМвЅвОцЈєЅвЈєЈЁ1Ј©ёщѕЭМвТвµГЈє
15ЎВ10%=150ЈЁГыЈ©Ј®
±ѕПоµчІйЦРПІ»¶Ў°ЕЬІЅЎ±µДС§ЙъИЛКэКЗЈ»150©Ѓ15©Ѓ45©Ѓ30=60ЈЁИЛЈ©Ј¬
ЛщХј°Щ·Ц±ИКЗЈє![]() ЎБ100%=40%Ј¬
ЎБ100%=40%Ј¬
»НјИзПВЈє
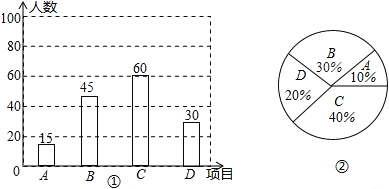
ЈЁ2Ј©УГA±нКѕДРЙъЈ¬B±нКѕЕ®ЙъЈ¬»НјИзПВЈє

№ІУР20ЦЦЗйїцЈ¬Н¬РФ±рС§ЙъµДЗйїцКЗ8ЦЦЈ¬
ФтёХєГійµЅН¬РФ±рС§ЙъµДёЕВККЗ![]() =
=![]() Ј®
Ј®


 јЖЛгёЯКЦПµБРґр°ё
јЖЛгёЯКЦПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄ№ШУЪxµДТ»ФЄ¶юґО·ЅіМx2©ЃЈЁ2k+1Ј©x+k2+2kЈЅ0УРБЅёцКµКэёщx1Ј¬x2Ј®
ЈЁ1Ј©ЗуКµКэkµДИЎЦµ·¶О§Ј®
ЈЁ2Ј©КЗ·сґжФЪКµКэkЈ¬К№µГx1x2©Ѓx12©Ѓx22ЈЅ©Ѓ16іЙБўЈїИфґжФЪЈ¬ЗлЗуіцkµДЦµЈ»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїПВБРНјРО¶јКЗУЙПаН¬µДРЎХэ·ЅРО°ґХХТ»¶Ё№жВЙ°Ъ·Е¶шіЙЈ¬ЖдЦРµЪ1ёцНј№ІУР3ёцРЎХэ·ЅРОЈ¬µЪ2ёцНј№ІУР8ёцРЎХэ·ЅРОЈ¬µЪ3ёцНј№ІУР15ёцРЎХэ·ЅРОЈ¬µЪ4ёцНј№ІУР24ёцРЎХэ·ЅРОЈ¬ЎЈ¬ХХґЛ№жВЙЕЕБРПВИҐЈ¬ФтµЪ8ёцНјЦРРЎХэ·ЅРОµДёцКэКЗЈЁЎЎЎЎЈ©
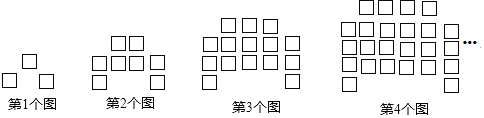
A. 48B. 63C. 80D. 99
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
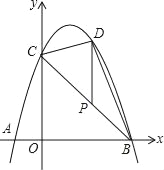
ЎѕМвДїЎїИзНјЈ¬ЕЧОпПЯy=©Ѓx2+bx+cѕ№эµгAЈ¬BЈ¬CЈ¬ТСЦЄµгAЈЁ©Ѓ1Ј¬0Ј©Ј¬µгCЈЁ0Ј¬3Ј©Ј®
ЈЁ1Ј©ЗуЕЧОпПЯµД±нґпКЅЈ»
ЈЁ2Ј©PОЄПЯ¶ОBCЙПТ»µгЈ¬№эµгPЧчyЦбµДЖЅРРПЯЈ¬Ѕ»ЕЧОпПЯУЪµгDЈ¬µ±ЎчBDCµДГж»эЧоґуК±Ј¬ЗуµгPµДЧш±кЈ»
ЈЁ3Ј©ЙиEКЗЕЧОпПЯЙПµДТ»µгЈ¬ФЪxЦбЙПКЗ·сґжФЪµгFЈ¬К№µГAЈ¬CЈ¬EЈ¬FОЄ¶ҐµгµДЛД±ЯРОКЗЖЅРРЛД±ЯРОЈїИфґжФЪЈ¬ЗуµгFµДЧш±кЈ»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
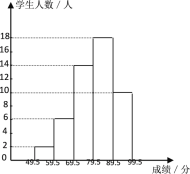
ЎѕМвДїЎїИзНјЈ¬ХвКЗДі°аКэС§їЖґъ±нёщѕЭЛыГЗ°аЙПС§ЖЪµДКэС§іЙјЁ»іцµДЖµКэ·ЦІјЦ±·ЅНјЈ¬ґУХвёцНјЦРЈ¬ЗлДг»ШґрПВБРОКМвЈє
ЈЁ1Ј©ДгИПОЄЛыГЗ°а№ІУРС§Йъ¶аЙЩГыЈї
ЈЁ2Ј©И«°аКэС§іЙјЁј°ёсВКЈЁ60·Цј°ТФЙПОЄј°ёсЈ©ОЄ¶аЙЩЈї
ЈЁ3Ј©ФЪДДёц·ЦКэ¶ОµДС§ЙъЧо¶аЈї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї¶ЁТеЈє¶ФЅЗ»ҐІ№ЗТУРТ»ЧйБЪ±ЯПаµИµДЛД±ЯРОіЖОЄЖжТмЛД±ЯРОЈ®
ЈЁ1Ј©ёЕДоАнЅвЈє
ФЪЖЅРРЛД±ЯРОЎўБвРОЎўѕШРОЎўХэ·ЅРОЦРЈ¬ДгИПОЄКфУЪЖжТмЛД±ЯРОµДУР__________ Ј»
ЈЁ2Ј©РФЦКМЅѕїЈє
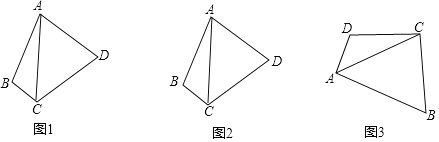
ўЩИзНј1Ј¬ЛД±ЯРОABCDКЗЖжТмЛД±ЯРОЈ¬AB=ADЈ¬ЗуЦ¤ЈєCAЖЅ·ЦЎПBCDЈ»
ўЪИзНј2Ј¬ЛД±ЯРОABCDКЗЖжТмЛД±ЯРОЈ¬AB=ADЈ¬ЎПBCD=2¦БЈ¬КФЛµГчЈєcos¦Б=![]() Ј»
Ј»
ЈЁ3Ј©РФЦКУ¦УГЈє
ИзНј3Ј¬ЛД±ЯРОABCDКЗЖжТмЛД±ЯРОЈ¬ЛДМх±ЯЦРЅцУРBC=CDЈ¬ЗТЛД±ЯРОABCDµДЦЬі¤ОЄ6+2![]() Ј¬ЎПBAC=45ЎгЈ¬AC=3
Ј¬ЎПBAC=45ЎгЈ¬AC=3![]() Ј¬ЗуЖжТмЛД±ЯРОABCDµДГж»эЈ®
Ј¬ЗуЖжТмЛД±ЯРОABCDµДГж»эЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ACКЗЎСOµДЦ±ѕ¶Ј¬BCКЗЎСOµДПТЈ¬µгPКЗЎСOНвТ»µгЈ¬Б¬ЅУPAЈ¬PBЈ¬ABЈ¬ТСЦЄЎПPBA=ЎПCЈ®

ЈЁ1Ј©ЗуЦ¤ЈєPBКЗЎСOµДЗРПЯЈ»
ЈЁ2Ј©Б¬ЅУOPЈ¬ИфOPЎОBCЈ¬ЗТOP=8Ј¬ЎСOµД°лѕ¶ОЄ![]() Ј¬ЗуBCµДі¤Ј®
Ј¬ЗуBCµДі¤Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
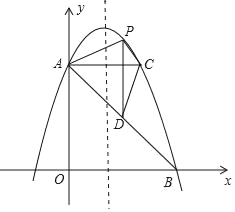
ЎѕМвДїЎїИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬Ц±ПЯyЈЅ©Ѓx+5УлyЦбЅ»УЪµгAЈ¬УлxЦбЅ»УЪµгBЈ®ЕЧОпПЯyЈЅ©Ѓx2+bx+c№эAЎўBБЅµгЈ®
ЈЁ1Ј©µгAЈ¬BµДЧш±к·Ц±рКЗAЎЎ ЎЎЈ¬BЎЎ ЎЎЈ»
ЈЁ2Ј©ЗуЕЧОпПЯµДЅвОцКЅЈ»
ЈЁ3Ј©№эµгAЧчACЖЅРРУЪxЦбЈ¬Ѕ»ЕЧОпПЯУЪµгCЈ¬µгPОЄЕЧОпПЯЙПµДТ»¶ЇµгЈЁµгPФЪACЙП·ЅЈ©Ј¬ЧчPDЖЅРРУЪyЦбЅ»ABУЪµгDЈ¬ОКµ±µгPФЪєОО»ЦГК±Ј¬ЛД±ЯРОAPCDµДГж»эЧоґуЈїІўЗуіцЧоґуГж»эЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬µгAєНµгBµДЧш±к·Ц±рОЄ![]() Ўў
Ўў![]() Ј¬ПЯ¶ОCDУлAB№ШУЪµг
Ј¬ПЯ¶ОCDУлAB№ШУЪµг![]() ЦРРД¶ФіЖЈ¬µгAЎўBµД¶ФУ¦µг·Ц±рОЄµгCЎўD
ЦРРД¶ФіЖЈ¬µгAЎўBµД¶ФУ¦µг·Ц±рОЄµгCЎўD
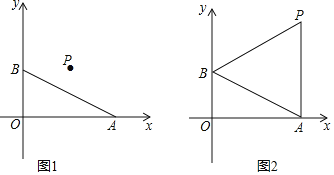
![]() µ±
µ±![]() К±Ј¬»іцПЯ¶ОCDЈ¬ІўЗуЛД±ЯРОABCDµДГж»эЈ»
К±Ј¬»іцПЯ¶ОCDЈ¬ІўЗуЛД±ЯРОABCDµДГж»эЈ»
![]() µ±
µ±![]() ______К±Ј¬ЛД±ЯРОABCDОЄХэ·ЅРОЈ»
______К±Ј¬ЛД±ЯРОABCDОЄХэ·ЅРОЈ»
![]() µ±
µ±![]() К±Ј¬Б¬ЅУPAЎўPBЈ¬ФЪOAЙПУРТ»µгMЈ¬ЗТ
К±Ј¬Б¬ЅУPAЎўPBЈ¬ФЪOAЙПУРТ»µгMЈ¬ЗТ![]() Ј¬ФтµгMµДЧш±кОЄ______Ј®
Ј¬ФтµгMµДЧш±кОЄ______Ј®
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com