
【题目】如图,在平面直角坐标系中,点A和点B的坐标分别为![]() 、
、![]() ,线段CD与AB关于点
,线段CD与AB关于点![]() 中心对称,点A、B的对应点分别为点C、D
中心对称,点A、B的对应点分别为点C、D
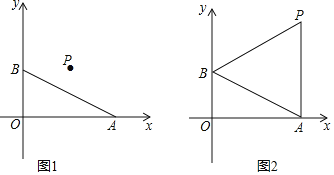
![]() 当
当![]() 时,画出线段CD,并求四边形ABCD的面积;
时,画出线段CD,并求四边形ABCD的面积;
![]() 当
当![]() ______时,四边形ABCD为正方形;
______时,四边形ABCD为正方形;
![]() 当
当![]() 时,连接PA、PB,在OA上有一点M,且
时,连接PA、PB,在OA上有一点M,且![]() ,则点M的坐标为______.
,则点M的坐标为______.
【答案】(1)图形见解析,2;(2)![]() 或
或![]() ;(3)
;(3) ![]() 或
或![]() .
.
【解析】
![]() 线段CD与AB关于点
线段CD与AB关于点![]() 中心对称,得出
中心对称,得出![]() ,
,![]() ,再根据对角线互相平分的四边形是平行四边形,证得四边形ABCD是平行四边形即可求出面积.
,再根据对角线互相平分的四边形是平行四边形,证得四边形ABCD是平行四边形即可求出面积.
![]() 根据四边形ABCD为正方形得出
根据四边形ABCD为正方形得出![]() ,
,![]() ,再根据A、B两点得坐标求得AB的长,从而求出PB的值,构建方程求出m即可.
,再根据A、B两点得坐标求得AB的长,从而求出PB的值,构建方程求出m即可.
![]() 如图3中,以PB为斜边作等腰直角三角形
如图3中,以PB为斜边作等腰直角三角形![]() ,以G为圆心,GB为半径作
,以G为圆心,GB为半径作![]() ,
,![]() 交x轴于M,
交x轴于M,![]() ,则
,则![]() 构造全等三角形求出点G坐标,再求出MH的值即可解决问题.
构造全等三角形求出点G坐标,再求出MH的值即可解决问题.
解:![]() 如图1中,
如图1中,
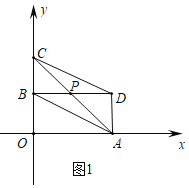
线段CD与AB关于点![]() 中心对称,
中心对称,
![]() ,
,![]() ,
,
![]() 四边形ABCD是平行四边形,
四边形ABCD是平行四边形,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
![]() 如图2中,
如图2中,
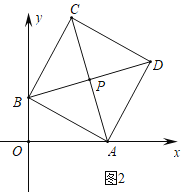
![]() 四边形ABCD是正方形,
四边形ABCD是正方形,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
解得![]() 或
或![]() ,
,
故答案为![]() 或
或![]() .
.
![]() 如图3中,以PB为斜边作等腰直角三角形
如图3中,以PB为斜边作等腰直角三角形![]() ,以G为圆心,GB为半径作
,以G为圆心,GB为半径作![]() ,
,![]() 交x轴于M,
交x轴于M,![]() ,则
,则![]() .
.
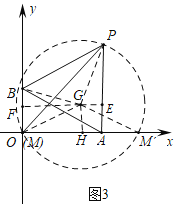
![]() ,
,![]() ,
,
![]() ,
,![]() ,设
,设![]() ,
,
作![]() 交PA于E,作
交PA于E,作![]() 于H,连接GM,
于H,连接GM,![]() .则
.则![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
可得![]() ,
,
解得![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,![]() .
.
故答案为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】(9分)为进一步推广“阳光体育”大课间活动,某中学对已开设的A实心球,B立定跳远,C跑步,D跳绳四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:
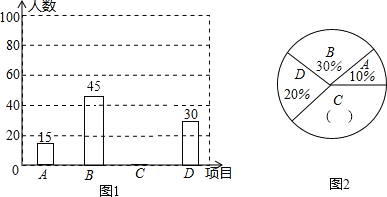
(1)请计算本次调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整;
(2)随机抽取了5名喜欢“跑步”的学生,其中有3名女生,2名男生,现从这5名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
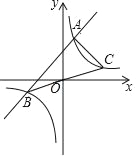
【题目】如图,已知函数y=x+2的图象与函数y=![]() (k≠0)的图象交于A、B两点,连接BO并延长交函数y=
(k≠0)的图象交于A、B两点,连接BO并延长交函数y=![]() (k≠0)的图象于点C,连接AC,若△ABC的面积为8.则k的值为_____.
(k≠0)的图象于点C,连接AC,若△ABC的面积为8.则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
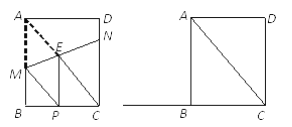
【题目】已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB上
(I)如图①,当EP⊥BC时,①求证CE=CN;②求CN的长;
(II)请写出线段CP的长的取值范围,及当CP的长最大时MN的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把图中阴影部分的小正方形移动一个,使它与其余四个阴影部分的正方形组成一个既是轴对称又是中心对称的新图形,这样的移法,正确的是( )

A. 6→3 B. 7→16 C. 7→8 D. 6→15
查看答案和解析>>
科目:初中数学 来源: 题型:
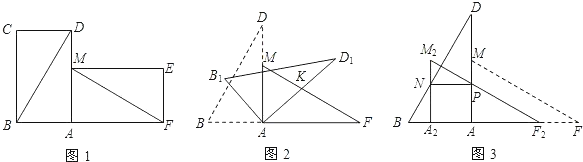
【题目】有两张完全重合的矩形纸片,小亮同学将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD、MF,若此时他测得BD=8cm,∠ADB=30度.请回答下列问题:(1)试探究线段BD与线段MF的关系,并简要说明理由;
(2)小红同学用剪刀将△BCD与△MEF剪去,与小亮同学继续探究.他们将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,请直接写出旋转角β的度数;
(3)若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为推动“时刻听党话 永远跟党走”校园主题教育活动,计划开展四项活动:A:党史演讲比赛,B:党史手抄报比赛,C:党史知识竞赛,D:红色歌咏比赛.校团委对学生最喜欢的一项活动进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2两幅不完整的统计图.请结合图中信息解答下列问题:
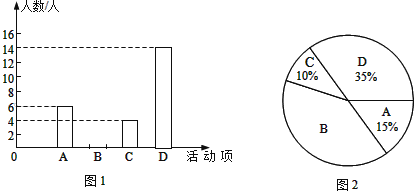
(1)本次共调查了 名学生;
(2)将图1的统计图补充完整;
(3)已知在被调查的最喜欢“党史知识竞赛”项目的4个学生中只有1名女生,现从这4名学生中任意抽取2名学生参加该项目比赛,请用画树状图或列表的方法,求出恰好抽到一名男生一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
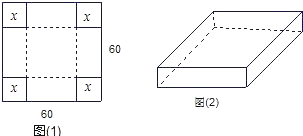
【题目】用一块边长为60㎝的正方形薄钢片制作一个长方体盒子:如果要做成一个没有盖的长方体盒子,可先在薄钢片的四个角上截去四个相同的小正方形,如图(1),然后把四边折合起来,如图(2)
(1)求做成的盒子底面积y(㎝2)与截去小正方形边长x(㎝)之间的函数关系式;
(2)当做成的盒子的底面积为900㎝2时,试求该盒子的容积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com