
【题目】用一块边长为60㎝的正方形薄钢片制作一个长方体盒子:如果要做成一个没有盖的长方体盒子,可先在薄钢片的四个角上截去四个相同的小正方形,如图(1),然后把四边折合起来,如图(2)
(1)求做成的盒子底面积y(㎝2)与截去小正方形边长x(㎝)之间的函数关系式;
(2)当做成的盒子的底面积为900㎝2时,试求该盒子的容积.
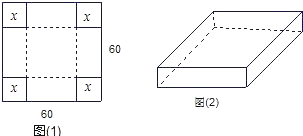
【答案】(1)y=4x2-240x+3600;(2)该盒子的容积为13500cm3.
【解析】
(1)先表示出盒子的正方形底面的边长,然后根据正方形的面积公式即可得出x,y的函数关系式;
(2)可将底面积代入(1)的式子中,求出高,然后根据底面积×高=容积,即可得出容积是多少.
(1)由题意可得y=(60-2x)2=4x2-240x+3600;
(2)当y=900时(60-2x)2 =900
∴60-2 x=±30
∴x1=15 x2=45
∵x2=45不符合题意∴x=15,
∴该盒子的容积为900×15=13500 (cm3),
答:该盒子的容积为13500cm3.
故答案为:(1)y=4x2-240x+3600;(2)该盒子的容积为13500cm3.


科目:初中数学 来源: 题型:
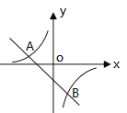
【题目】如图,在平面直角坐标系中,点A和点B的坐标分别为![]() 、
、![]() ,线段CD与AB关于点
,线段CD与AB关于点![]() 中心对称,点A、B的对应点分别为点C、D
中心对称,点A、B的对应点分别为点C、D
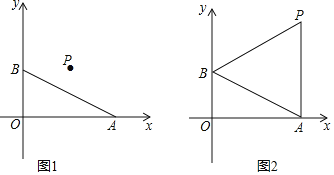
![]() 当
当![]() 时,画出线段CD,并求四边形ABCD的面积;
时,画出线段CD,并求四边形ABCD的面积;
![]() 当
当![]() ______时,四边形ABCD为正方形;
______时,四边形ABCD为正方形;
![]() 当
当![]() 时,连接PA、PB,在OA上有一点M,且
时,连接PA、PB,在OA上有一点M,且![]() ,则点M的坐标为______.
,则点M的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在ABCD中,O为对角线BD的中点.过O的直线MN交直线AB于点M,交直线CD于点N;过O的另一条直线PQ交直线AD于点P,交直线BC于点Q,连接PN、MQ.
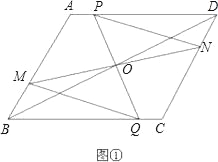
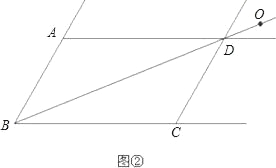
(1)试证明△PON与△QOM全等;
(2)若点O为直线BD上任意一点,其他条件不变,则△PON与△QOM又有怎样的关系?试就点O在图②所示的位置,画出图形,证明你的猜想;
(3)若点O为直线BD上任意一点(不与点B、D重合),设OD:OB=k,PN=x,MQ=y,则y与x之间的函数关系式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近期猪肉价格不断走高,引起市民与政府的高度关注,当市场猪肉的平均价格达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.
(1)从今年年初至5月20日,猪肉价格不断走高,5月20日比年初价格上涨了60%,某市民在今年5月20日购买2.5千克猪肉至少要花100元钱,那么今年年初猪肉的最低价格为每千克多少元?
(2)5月20日猪肉价格为每千克40元,5月21日,某市决定投入储备猪肉,并规定其销售价格在5月20日每千克40元的基础上下调a%出售,某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格仍为40元的情况下,该天的两种猪肉总销量比5月20日增加了a%,且储备猪肉的销量占总销量的![]() ,两种猪肉销售的总金额比5月20日提高了
,两种猪肉销售的总金额比5月20日提高了![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.
(1)求证:AE与⊙O相切于点A;
(2)若AE∥BC,BC=2![]() ,AC=2
,AC=2![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 图象交于A(-2,1)、B(1,n)两点.
图象交于A(-2,1)、B(1,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
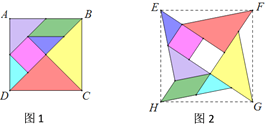
【题目】七巧板是我们祖先的一项卓越创造,被西方人誉为“东方魔板”.下面的两幅图正方形(如图1)、“风车型”(如图2)都是由同一副七巧板拼成的,则图中正方形ABCD,EFGH的面积比为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
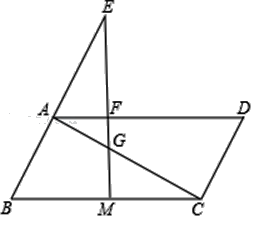
【题目】已知,如图,在平行四边形ABCD中,M是BC边的中点,E是边BA延长线上的一点,连结EM,分别交线段AD、AC于点F、G.
(1)求证:![]() ;
;
(2)当BC2=2BABE时,求证:∠EMB=∠ACD.
查看答案和解析>>
科目:初中数学 来源: 题型:
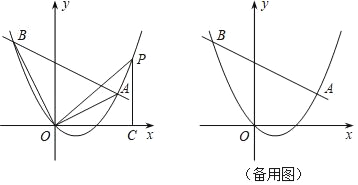
【题目】如图,在平面直角坐标系中,直线y=kx﹣4k+4与抛物线y=![]() x2﹣x交于A、B两点.
x2﹣x交于A、B两点.
(1)直线总经过定点,请直接写出该定点的坐标;
(2)点P在抛物线上,当k=﹣![]() 时,解决下列问题:
时,解决下列问题:
①在直线AB下方的抛物线上求点P,使得△PAB的面积等于20;
②连接OA,OB,OP,作PC⊥x轴于点C,若△POC和△ABO相似,请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com