
| 甲成绩(分) | 76 | 84 | 90 | 86 | 81 | 87 | 86 | 82 | 85 | 83 |
| 乙成绩(分) | 82 | 84 | 85 | 89 | 79 | 80 | 91 | 89 | 74 | 79 |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
| 优秀人数 |
| 总人数 |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
. |
| x |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:阅读理解
| 字母 | A | B | C | D | E | F | G | H | I | J | K | L | M |
| 明码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 字母 | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| 明码 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 13 | 24 | 25 | 26 |
| 汉字 | 自 | 信 | |||
| 拼音 | Z | I | X | I | N |
| 明码:x | 26 | 9 | 24 | 9 | 14 |
密钥:y= | |||||
| 密码:y | 91 | 40 | |||
| 汉字 | 自 | 信 | |||
| 拼音 | Z | I | X | I | N |
| 明码:x | 26 | 9 | 24 | 9 | 14 |
密钥:y=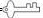 | |||||
| 密码:y | 70 | 36 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
| 甲成绩(分) | 76 | 84 | 90 | 86 | 81 | 87 | 86 | 82 | 85 | 83 |
| 乙成绩(分) | 82 | 84 | 85 | 89 | 79 | 80 | 91 | 89 | 74 | 79 |
| . |
| x |
| . |
| x |
| . |
| x |
| . |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com